Axial Load Capacities for Single Plates Calculator | Engineers Edge | www.engineersedge.com

Membership Services

Axial Load Capacities for Single Plates Engineering Calculator

Mechanics Machines Menu

Beam Deflection and Stress Calculators

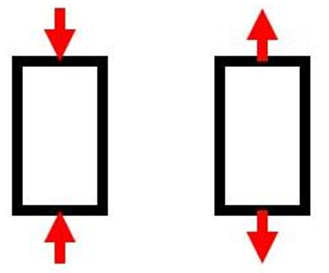
Axial Load Capacities for Single Plates: Based on Gross Section Loaded Uniformly in Either Tension or Compression per AISC 9th Edition Manual (ASD)

Home
Engineering Book Store
Engineering Forum
Applications and Design
Beam Deflections and Stress
Bearing Apps, Specs & Data
Belt Design Data Calcs
Civil Engineering
Design & Manufacturability
Electric Motor Alternators
Engineering Calculators
Excel App. Downloads
Flat Plate Stress Calcs
Fluids Flow Engineering
Friction Engineering
Gears Design Engineering
General Design Engineering
Hardware, Imperial, Inch
Hardware, Metric, ISO
Heat Transfer
Hydraulics Pneumatics
HVAC Systems Calcs
Economics Engineering
Electronics Instrumentation
Engineering Mathematics
Engineering Standards
Finishing and Plating
Friction Formulas Apps
Lubrication Data Apps
Machine Design Apps
Manufacturing Processes
Materials and Specifications
Mechanical Tolerances Specs
Plastics Synthetics
Power Transmission Tech.
Pressure Vessel
Pumps Applications
Re-Bar Shapes Apps
Section Properties Apps
Strength of Materials
Spring Design Apps
Structural Shapes
Threads & Torque Calcs
Thermodynamics
Physics
Vibration Engineering
Videos Design Manufacture
Volume of Solids Calculators
Welding Stress Calculations
Training Online Engineering

Copyright Notice