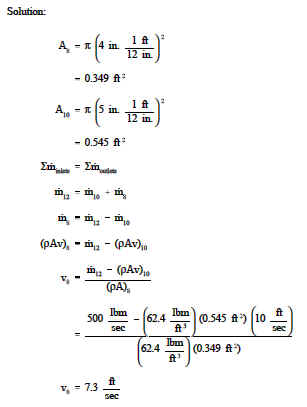|
Fluid
Flow Table of Contents
The continuity equation is simply a
mathematical expression of the principle of conservation of mass. For a control volume that
has a single inlet and a single outlet, the principle of conservation of mass states
that, for steady-state flow, the mass flow rate into the
volume must equal the
mass flow rate out. The continuity equation for this
situation is expressed by Equation 3-5.
For a control volume with multiple inlets and
outlets, the principle of conservation of mass requires
that the sum of the mass flow rates into the control volume
equal the sum of the mass flow
rates out of the control volume. The continuity equation for
this more general situation is expressed
by Equation 3-6.
One of the simplest applications of the
continuity equation is determining the change in fluid velocity due to an expansion or
contraction in the diameter of a pipe.
Example:
Continuity Equation - Piping Expansion
Steady-state flow exists in a pipe that
undergoes a gradual expansion from a diameter of 6
in. to a diameter of 8 in. The density of the fluid in the
pipe is constant at 60.8 lbm/ft3. If the flow velocity is 22.4
ft/sec in the 6 in. section, what is the flow velocity in the
8 in. section?
Solution:
From the continuity equation we know that the
mass flow rate in the 6 in. section must equal
the mass flow rate in the 8 in. section. Letting the
subscript 1 represent the 6 in. section
and 2 represent the 8 in. section we have the following.
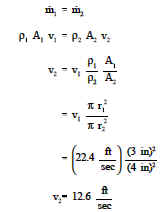
So by using the
continuity equation, we find that the increase in pipe
diameter from 6 to 8 inches caused a decrease in flow
velocity from 22.4 to 12.6 ft/sec.
The continuity equation can also be used to
show that a decrease in pipe diameter will cause an increase
in flow velocity.
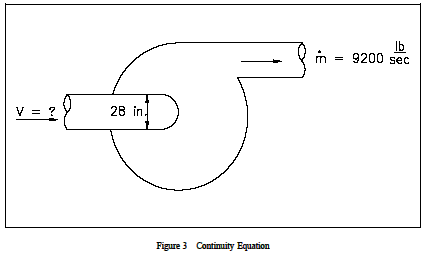
Example:
Continuity Equation - Centrifugal Pump The
inlet diameter of the reactor coolant pump shown in Figure 3
is 28 in. while the outlet
flow through the pump is 9200 lbm/sec. The density of the
water is 49 lbm/ft3. What is the velocity at the pump
inlet?
The above example indicates that the flow
rate into the system is the same as that out of the system.
The same concept is true even though more than one flow path
may enter or leave the system
at the same time. The mass balance is simply adjusted to
state that the sum of all flows entering
the system is equal to the sum of all the flows leaving the
system if steady-state conditions
exist. An example of this physical case is included in the
following example.
Example:
Continuity Equation - Multiple Outlets
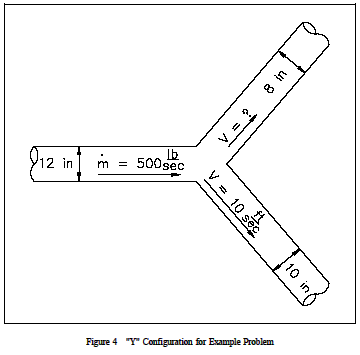
A piping system has a "Y"
configuration for separating the flow as shown in Figure 4. The diameter of the inlet leg is
12 in., and the diameters of the outlet legs are 8 and 10 in. The velocity in the 10 in.
leg is 10 ft/sec. The flow through the main portion is 500
lbm/sec. The density of water is
62.4 lbm/ft3.
What is the velocity out of the 8 in. pipe section?
|
