Related Resources: math
Circular Segment Equation and Calculator
Circular Segment Equation and Calculator
Circular segment is a region of a circle which is "cut off" from the rest of the circle by a secant or a chord . More formally, a circular segment is a region of two-dimensional space that is bounded by an arc (of less than 180°) of a circle and by the chord connecting the endpoints of the arc.
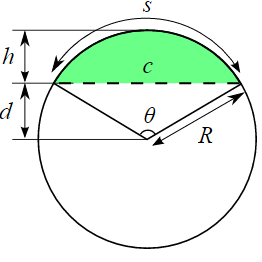
Where:
Radius:
R = h + d = h / 2 + c2 / ( 8h )
Arc Length:
s = arcsin ( c / ( h + c2 / 4h ) ) ( h + c2 / 4h )
Chord Length: θ given in radians.
c = 2 R sin ( θ / 2 )
Angle:
θ = 2 arctan ( c / ( 2 d ) )
Sagitta: θ given in radians.
h = R ( 1 - cos ( θ / 2) )
Area:
The area A of the circular segment is equal to the area of the circular sector minus the area of the triangular portion. θ given in radians.
A = (R2 / 2 ) ( θ - sinθ )
Central angle in radians
A = ( R2 / 2 ) ( ( α Π ) / 180° - sinθ )
Central angle in degrees