Strength of Materials Basics and Equations | Mechanics of Materials Equations
|
Strength / Mechanics of Material Menu Strength of materials, also called mechanics of materials, is a subject which deals with the behavior of solid objects subject to stresses and strains . In materials science, the strength of a material is its ability to withstand an applied load without failure. A load applied to a mechanical member will induce internal forces within the member called stresses when those forces are expressed on a unit basis. The stresses acting on the material cause deformation of the material in various manner. Deformation of the material is called strain when those deformations too are placed on a unit basis. The applied loads may be axial (tensile or compressive), or shear . The stresses and strains that develop within a mechanical member must be calculated in order to assess the load capacity of that member. This requires a complete description of the geometry of the member, its constraints, the loads applied to the member and the properties of the material of which the member is composed. With a complete description of the loading and the geometry of the member, the state of stress and of state of strain at any point within the member can be calculated. Once the state of stress and strain within the member is known, the strength (load carrying capacity) of that member, its deformations (stiffness qualities), and its stability (ability to maintain its original configuration) can be calculated. The calculated stresses may then be compared to some measure of the strength of the member such as its material yield or ultimate strength. The calculated deflection of the member may be compared to a deflection criteria that is based on the member's use. The calculated buckling load of the member may be compared to the applied load. The calculated stiffness and mass distribution of the member may be used to calculate the member's dynamic response and then compared to the acoustic environment in which it will be used. Material strength refers to the point on the engineering stress–strain curve (yield stress) beyond which the material experiences deformations that will not be completely reversed upon removal of the loading and as a result the member will have a permanent deflection. The ultimate strength refers to the point on the engineering stress–strain curve corresponding to the stress that produces fracture. The following are basic definitions and equations used to calculate the strength of materials. Stress (normal) Stress is the ratio of applied load to the cross-sectional area of an element in tension and isexpressed in pounds per square inch (psi) or kg/mm2.
Strain (normal) A measure of the deformation of the material that is dimensionless.
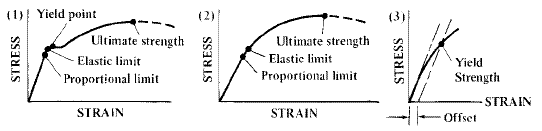
Stress Strain Curve Proportional limit is the point on a stress-strain curve at which it begins to deviate from the straight-line relationship between stress and strain. See accompanying figure at (1 & 2). Elastic limit is the maximum stress to which a specimen may be subjected and still return to its original length upon release of the load. A material is said to be stressed within the elastic region when the working stress does not exceed the elastic limit, and to be stressed in the plastic region when the working stress does exceed the elastic limit. The elastic limit for steel is for all practical purposes the same as its proportional limit. See accompanying figure at (1, 2). Yield point is a point on the stress-strain curve at which there is a sudden increase in strain without a corresponding increase in stress. Not all materials have a yield point. See accompanying figure at (1). Yield strength, Sy, is the maximum stress that can be applied without permanent deformation of the test specimen. This is the value of the stress at the elastic limit for materials for which there is an elastic limit. Because of the difficulty in determining the elastic limit, and because many materials do not have an elastic region, yield strength is often determined by the offset method as illustrated by the accompanying figure at (3). Yield strength in such a case is the stress value on the stress-strain curve corresponding to a definite amount of permanent set or strain, usually 0.1 or 0.2 per cent of the original dimension. Modulus of elasticityMetal deformation is proportional to the imposed loads over a range of loads. Since stress is proportional to load and strain is proportional to deformation, this implies that stress is proportional to strain. Hooke's Law is the statement of that proportionality.
The constant, E, is the modulus of elasticity, Young's modulus or the tensile modulus and is the material's stiffness. Young's modulus is in terms of 106 psi or 103 kg/mm2. If a material obeys Hooke's Law it is elastic. The modulus is insensitive to a material's temper. Normal force is directly dependent upon the elastic modulus. Proportional limit The greatest stress at which a material is capable of sustaining the applied load without deviating from the proportionality of stress to strain. Expressed in psi (kg/mm2). Ultimate strength (tensile)The maximum stress a material withstands when subjected to an applied load. Dividing the load at failure by the original cross sectional area determines the value. Elastic limitThe point on the stress-strain curve beyond which the material permanently deforms after removing the load . Yield strengthPoint at which material exceeds the elastic limit and will not return to its origin shape or length if the stress is removed. This value is determined by evaluating a stress-strain diagram produced during a tensile test. Poisson's ratioThe ratio of the lateral to longitudinal strain is Poisson's ratio for a given material.
Poisson's ratio is a dimensionless constant used for stress and deflection analysis of structures such as beams, plates, shells and rotating discs.
Bending stressWhen bending a piece of metal, one surface of the material stretches in tension while the opposite surface compresses. It follows that there is a line or region of zero stress between the two surfaces, called the neutral axis. Make the following assumptions in simple bending theory:
Using classical beam formulas and section properties, the following relationship can be derived:
The reported flexural modulus is usually the initial modulus from the stress-strain curve in tension. The maximum stress occurs at the surface of the beam farthest from the neutral surface (axis) and is:
For a rectangular cantilever beam with a concentrated load at one end, the maximum surface stress is given by:
YieldingYielding occurs when the design stress exceeds the material yield strength. Design stress is typically maximum surface stress (simple loading) or Von Mises stress (complex loading conditions). The Von Mises yield criterion states that yielding occurs when the Von Mises stress,
where σ1, σ2, σ3 are principal stresses. Safety factor is a function of design stress and yield strength. The following equation denotes safety factor, fs.
Where YS is the Yield Strength and DS is the Design Stress See our Material Terms and Links page for additional information. Related:
Link to this Webpage: © Copyright 2000 -
2024, by Engineers Edge, LLC |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||