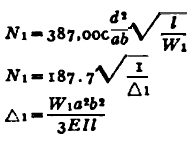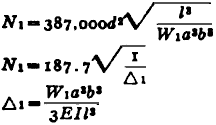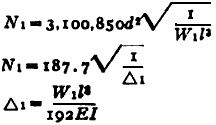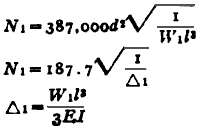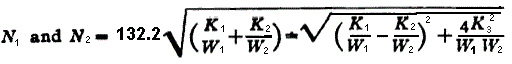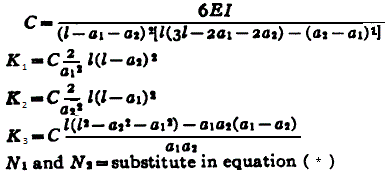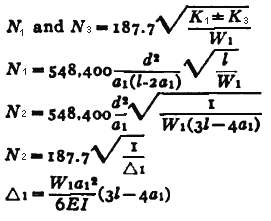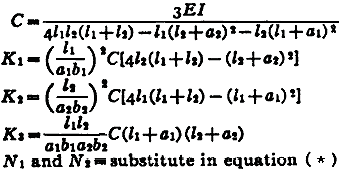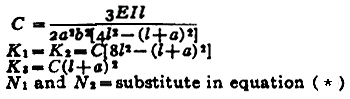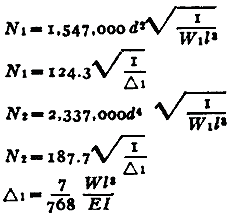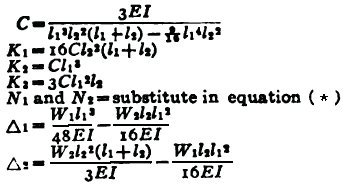Critical Speeds of Rotating Shafts with Single Loads Equations and Calculators
Bearings
Application Knowledge Menu
Critical Speeds of Rotating Shafts or Mass Review
Critical Speeds of Rotating Shafts with Single Loads: When calculating critical speeds, the weight or mass of the rotating cylinder or shaft is assumed to be zero or add 1/2 to 2/3 of the rotating shaft to the load mass. Keep in mind that a shaft with more than one load or distributed loads may have an infinite number of critical speeds. Typically, the first critical speed is most important for your design.
NOTE: All Calculators require a Premium Membership to access.
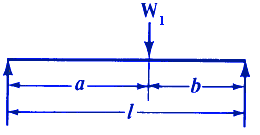
Load Configuration |
Equation |
 |
|
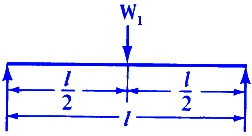 |
|
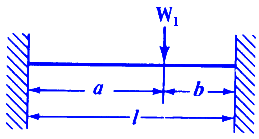 |
|
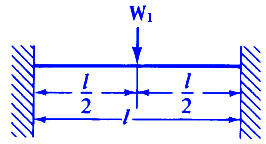 |
|
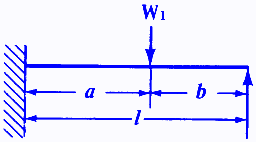 |
|
 |
|
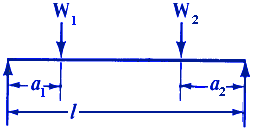
| Two Concentrated Loads General Equation *
|
|
 |
|
 |
|
 |
|
 |
|
 |
|
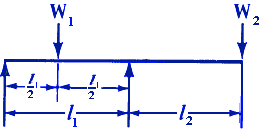 |
|
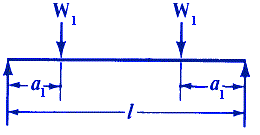
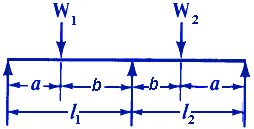
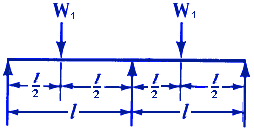
Where:
| N1 | = first critical speed, RPM |
| N2 | = second critical speed, RPM |
| Δ1 | = static deflection, (in, m) at W1 if shaft is horizontal |
| Δ2 | = static deflection, (in, m) at W2 if shaft is horizontal |
| E | = modulus of elasticity (young's modulus), (psi, N/m2) |
| d | = diameter of shaft, (inches, m) |
| W1 | = load applied to shaft, (lbs, Kg) |
| I | = Area Moment of Inertia , (in4, m4) |
| l | = distance between centers of bearings, (inches, m) |
| a | = distance from bearings to load, (inches, m) |
| b | = distance from bearings to load, (inches, m) |
Related Resources: