Counterbalancing Several Masses Located in a Single Plane Formulas and Calculator

Related Resources: calculators

Counterbalancing Several Masses Located in a Single Plane Formulas and Calculator

Engineering Materials
Tolerances, Engineering Design Limits ans Fits

Counterbalancing Several Masses Located in a Single Plane Formulas and Calculator

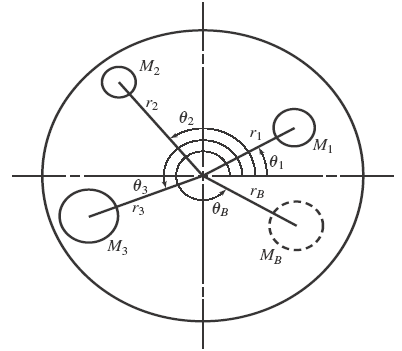
In all balancing problems, the product of the counterbalancing mass (or weight) and its radius are calculated; it is thus necessary to select either the mass or the radius and then calculate the other value from the product of the two quantities. Design considerations usually make this decision self-evident. The angular position of the counterbalancing mass must also be calculated.

Counterbalancing Several Masses

Calculator requires a Premium membership
Preview Counterbalancing Several Masses Located in a Single Plane Calculator

Counterbalancing Several Masses Located in a Single Plane can be calculated by the following formulas:

Eq :

M_B r_B = [ ( ∑ M r cosθ )² + ( ∑ M r sinθ )² ]^1/2

tanθ_B = - ( ∑ M r sinθ) / - ( ∑ M r cosθ ) = - y / - x

Image and Table 1
Relationship of Angle Function Signs to Quadrant in Which They Occur

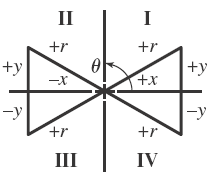
Angle θ
Trigonmetric Function	0° to 90°	90° to 180°	180° to 270°	270° to 360°
Trigonmetric Function	Signs of the Functions
tan	+y / +x	+y / -x	-y / -x	-y / +x
sine	+y / +r	+y / +r	-y / +r	-y / +r
cosine	+x / +r	-x / +r	-x / +r	+x / +r

Where:

M₁, M₂, M₃, ..., M_n = any unbalanced mass or weight, (kg, lb),
M_B = counterbalancing mass or weight, (kg, lb),
r = radius to center of gravity of any unbalance mass or weitgh, (mm, in),
r_B = radius to center of gravity of counterbalancing mass or weight, (mm, in),
θ = angular position of r of any unbalanced mass or weight, (degrees),
θ_B = angular position of r_B of counterbalancing mass or weight, degrees

Reference:

Machinery's Handbook 30th edition