Related Resources: calculators
Hertz Gear Tooth Contact Stress Equation and Calculator
Hertz Gear Tooth Contact Stress Equation and Calculator
Gears are one of the oldest of humanity’s inventions. Nearly all the devices we think of as machines utilize gearing of one type or another. Nevertheless, the design or specification of a gear is only part of the overall system design picture. From industry’s standpoint, gear transmission systems are considered one of the critical aspects of Contact Stress Analysis.
The transfer of power between gears takes place at the contact between the acting teeth. The stresses at the contact point can be computed by means of the theory of Hertz. The theory provides mathematical expressions of stresses and deformations of curved bodies in contact.
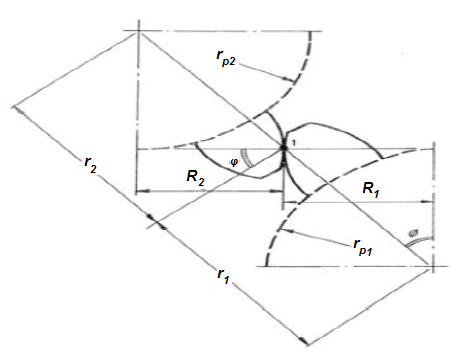
Preview: Hertz Gear Tooth Contact Stress Calculator
The Hertz theory equation assumes an elliptic stress distribution
σo = {( W ( 1 + rp1 / rp2 ) )/( rp1 F π [ ( 1 - v12 ) / E1 + ( 1 - v22 ) / E2 ] sinφ )} 0.5
Where:
σo = Maximum value of contact stress (N/mm2)
W = force pressing the two gear teeth together (N)
rp1 & rp2 = Pitch radii of the pinion and gear (mm)
φ = pressure angle (deg.)
F = Face width of pinion (mm)
d1, d2 = diameters of two cylinders (mm)
E1, E2 = modulii of elasticity of two cylinder materials (N/mm2)
μ1, μ2 = Poisson’s ratio of the two cylinder materials (Unit less)
References:
International Journal of Modern Studies in Mechanical Engineering (IJMSME) VOlume 1, Issue 1, June 2015, PP 45-52
Putti Srinivasa Rao1, Professor, Dept. of Mechanical Engineering, Andhra University College of Engineering (A), Visakhapatnam, Andhra Pradesh, India.
Nadipalli Sriraj, Mohammad Farookh, B.E Project Students, Dept. of Mechanical Engineering, Andhra University College of Engineering