Poiseuille Law Formula and Calculator

Related Resources: calculators

Poiseuille Law Formula and Calculator

Fluid Flow Hydraulic and Pneumatic Engineering and Design

Poiseuille's Law Formula and Calculator

This equation is known as Poiseuille’s law, and this flow is called Hagen - Poiseuille flow in honor of the works of G. Hagen (1797–1884) and J. Poiseuille (1799–1869) on the subject. Note from Eq. 1,2 and 3 that for a specified flow rate, the pressure drops and thus the required pumping power is proportional to the length of the pipe and the viscosity of the fluid, but it is inversely proportional to the fourth power of the radius (or diameter) of the pipe.

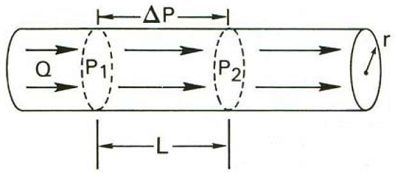
The relationship between pressure and continuous laminar flow of fluid in a rigid tube is described by Poiseuille's law, which states that the flow rate of a fluid, Q, is directly proportional to the pressure difference, along the length of the tube and the fourth power of the radius of the tube, and inversely proportional to the tube length, and fluid viscosity.

The assumptions of the equation are that the fluid is incompressible and Newtonian; the flow is laminar through a pipe of constant circular cross-section that is substantially longer than its diameter; and there is no acceleration of fluid in the pipe. For velocities and pipe diameters above a threshold, actual fluid flow is not laminar but turbulent, leading to larger pressure drops than calculated by the Hagen - Poiseuille equation.

Poiseuille's Law Formula and Calculator

Eq 1
Q = ( π ΔP r⁴ ) / ( 8 η l )

Eq 2
Q = [ ( P₁ - P₂ ) π r⁴ ] / ( 8 η l )

Eq 3
Q = [ ( P₁ - P₂ ) π D⁴ ] / ( 128 η l )

Breaking the formula down:

Q = ( P₁ - P₂ ) / r = Volume Flow Rate

r = ( 8 η l ) / ( π r⁴ ) = Resistance to flow

Where:

Q = flow rate,
ΔP = pressure gradieant between the two ends of the pipe,
P₁ = initial pressure,
P₂ = Final pressure,
r = radius of pipe,
l = length of the pipe,
η = viscosity (dynamic) of fluid.

Source:

Fluid Mechanics
Seventh Edition
Frank M. White
University of Rhode Island