Related Resources: calculators
Space Time Pythagorean Theorem Formulae and Calculator
Geometry of Causality Space Time (Space Time Pythagorean Theorem)
(Just little webpage and calculator written by a non-physicist born out of curiosity.)
In special relativity, the distance between two points is no longer the same if it measured by two different observers when one of the observers is moving, because of the Lorentz contraction.
But special relativity provides a new invariant, called the spacetime interval, which combines distances in space and in time. All observers who measure time and distance carefully will find the same spacetime interval between any two events.
Three dimension Space between two points defined by Pythagorean Theorem
(Δd)2 = (Δx)2 + (Δy)2+ (Δz)2
Four Dimensional Space - Time
(Δs)2 = (Δx)2 - (cΔt)2
Three space dimensions spacetime interval
(Δs)2 = (cΔt)2 - (Δx)2 - (Δy)2- (Δz)2
Alternate sign convention three space dimensions
(Δs)2 = -(cΔt)2 + (Δx)2 + (Δy)2 + (Δz)2
The sign conventions are associated with the metric signatures (+ − − −) and (− + + +). A minor variation is to place the time coordinate last rather than first. Both conventions are widely used within the field of study.
Where:
Δs = space time interval (m),
Δx = distance traveled as seen by some observer (m),
Δy = distance traveled as seen by some observer (m),
Δz = distance traveled as seen by some observer (m),
Δt = time taken as seen by some observer (sec),
c = speed of light (299,792,458 m/s).
If (Δs)2 is positive, the spacetime interval is timelike , meaning that two events are separated by more time than space. If (Δs)2 is negative, the spacetime interval is spacelike , meaning that two events are separated by more space than time.
Spacetime intervals are zero when x = cΔt which indicates that the spacetime interval between two events on the world line of something moving at the speed of light is zero. ( A photon arriving in our eye from a distant star will not have aged, despite having (from our perspective) spent years in its passage.)
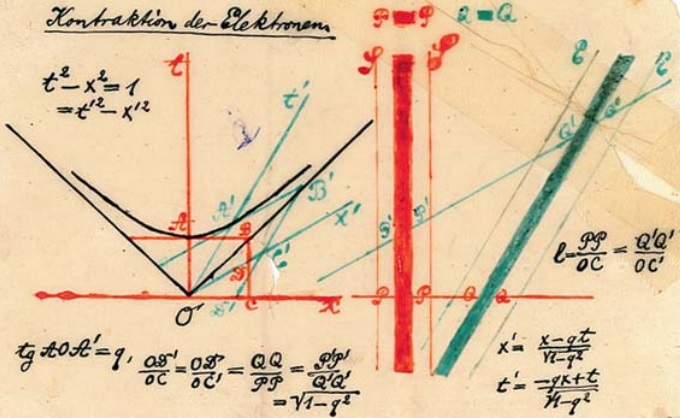
Hand-colored transparency presented by Minkowski in his 1908 Raum und Zeit lecture
Related:
- Relativity Theory and Astrophysics , Relativity and Cosmology
- Einstein's Theory of Relativity
- Relativity and Reference Frames
Link to this Webpage:
© Copyright 2000 -
2024, by Engineers Edge, LLC
www.engineersedge.com
All rights reserved
Disclaimer |
Feedback
Advertising
| Contact
