Ideal Pinned Column Buckling Equation and Calculation, Euler's Formula

Mechanics of Materials Menu

For the ideal pinned column shown in below, the critical buckling load can be calculated using Euler's formula:

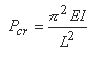
Open: Ideal Pinned Column Buckling Calculator

Where:

E = Modulus of elasticity of the material

I = Minimum moment of inertia

L = Unsupported length of the column (see picture below) 

Note that regardless of the end condition, the critical load depends not on the material strength, but rather the flexural rigidity, EI. Buckling resistance can be increased by increasing the moment of inertia.

When a column buckles, it maintains its deflected shape after the application of the critical load. In most applications, the critical load is usually regarded as the maximum load sustainable by the column. Theoretically, any buckling mode is possible, but the column will ordinarily deflect into the first mode. A column will buckle when the load P reaches a critical level, called the critical load, P_cr. 

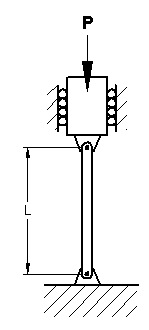
Ideal Pinned Column (Pinned - Pinned)

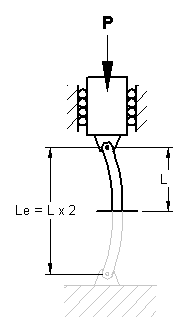
For columns with different types of support, Euler's formula may still be used if the distance L is replaced with the distance between the zero moment points. See "Effective Length Constant Table" below. 

This length is called the effective length Le and is illustrated in below. Thus the critical load equation becomes: 

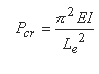
The slenderness ratio is an important parameter in the classification of compression members, and is represented by the equation:

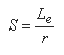
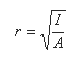
Where:

r = Radius of gyration

I = Moment of inertia

A = Area cross section

If the slenderness ratio > (greater than) critical slenderness ratio, then the column is treated as a long column and the Euler buckling formula is applicable.

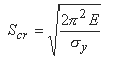
If slenderness ratio is < (less than) the critical slenderness ratio, the column is treated as a short column. 

In short columns, failure may occur by compression without significant buckling and at stresses exceeding the proportional limit. For this condition, Johnson's formula is applicable:

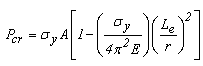
For columns that fail subsequent to the onset of inelastic behavior, the constant of proportionality must be used rather than the modulus of elasticity (Engesser formula). The constant of proportionality, Et, is the slope of the stress-strain diagram beyond the proportional limit, termed the tangent modulus. Note within the linearly elastic range, E = Et.

** In practice, the Effective Length Constant is increased by a factor approximately 10 - 20 %

© Copyright 2000 - 2012, by Engineers Edge, LLC All rights reserved.
Disclaimer

Home
Engineering Store
Engineering Training PDH
Products & Services
Engineering Forum
Engineering Design Data
Engineering News
Engineering Videos
Engineering Calculators
Engineering Jobs
Industrial News Buzz
Newsletter Register
Feedback
GD&T Training ASME Y14.5-2009
DFM Training
Contribute Article

Copyright Notice