Ideal Fluid Theory - Fluid Flow
Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
An ideal fluid (also called Perfect Fluid) is one that is incompressible and has no viscosity. Ideal fluids do not actually exist, but sometimes it is useful to consider what would happen to an ideal fluid in a particular fluid flow problem in order to simplify the problem.
Real fluids are "sticky" and contain (and conduct) heat. Perfect fluids are idealized models in which these possibilities are neglected. Specifically, perfect fluids have no shear stresses, viscosity, or heat conduction.
In space-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form:
![]()
Where U is the velocity vector field of the fluid and where:
![]()
is the metric tensor of Minkowski spacetime.
In time-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form:
![]()
Where U is the velocity vector field of the fluid and where:
![]()
is the metric tensor of Minkowski spacetime This takes on a particularly simple form in the rest frame:
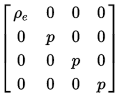
where:
![]()
is the energy density and p is the pressure of the fluid.
Perfect fluids admit a Lagrangian formulation, which allows the techniques used in field theory, in particular, quantization, to be applied to fluids. This formulation can be generalized, but unfortunately, heat conduction and anisotropic stresses cannot be treated in these generalized formulations.
Perfect fluids are often used in general relativity to model idealized distributions of matter, such as the interior of a star or an isotropic universe. In the latter case, the equation of state of the perfect fluid may be used in Friedmann–Lemaître–Robertson–Walker equations to describe the evolution of the universe.