Related Resources: manufacturing
Brinell Hardness Test Equation and Calculator
Engineering Materials and Applications
Brinell Hardness Test Equations, Calculators and Review
The Brinell hardness test uses a hardened steel ball indenter that is pushed into the material under a specified force. The diameter of the indentation left in the surface of the material is measured and a Brinell hardness number is calculated from this diameter.
Hardness tests serve an important need in industry even though they do not measure a unique quality that can be termed hardness. The tests are empirical, based on experiments and observation, rather than fundamental theory. Its chief value is as an inspection device, able to detect certain differences in material when they arise even though these differences may be undefinable. For example, two lots of material that have the same hardness may or may not be alike, but if their hardness is different, the materials certainly are not alike.
Several methods have been developed for hardness testing. Those most often used are Brinell, Rockwell, Vickers, Tukon, Sclerscope, and the files test. The first four are based on indentation tests and the fifth on the rebound height of a diamond-tipped metallic hammer. The file test establishes the characteristics of how well a file takes a bite on the material.
The Brinell scale characterizes the indentation hardness of materials through the scale of penetration of an indenter, loaded on a material test-piece. It is one of several definitions of hardness in materials science.
The typical brinell hardness test uses a 10 millimeters (0.39 in) diameter steel ball as an indenter with a 3,000 kgf (29 kN; 6,600 lbf) force. For softer materials, a smaller force is used; for harder materials, a tungsten carbide ball is substituted for the steel ball. The indentation is measured and hardness calculated as:
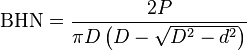
where:
P = applied force (kgf)
D = diameter of indenter (mm)
d = diameter of indentation (mm)
The BHN can be converted into the ultimate tensile strength (UTS), although the relationship is dependent on the material, and therefore determined empirically. The relationship is based on Meyer's index (n) from Meyer's law. If Meyer's index is less than 2.2 then the ratio of UTS to BHN is 0.36. If Meyer's index is greater than 2.2, then the ratio increases.
BHN is designated by the most commonly used test standards (ASTM E10-12 and ISO 6506–1:2005) as HBW (H from hardness, B from brinell and W from the material of the indenter, tungsten (wolfram) carbide). In former standards HB or HBS were used to refer to measurements made with steel indenters.
HBW is calculated in both standards using the SI units as:
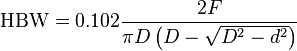
where:
- F = applied force (N)
- D = diameter of indenter (mm)
- d = diameter of indentation (mm)
When quoting a Brinell hardness number (BHN or more commonly HB), the conditions of the test used to obtain the number must be specified. The standard format for specifying tests can be seen in the example "HBW 10/3000". "HBW" means that a tungsten carbide (from the chemical symbol for tungsten) ball indenter was used, as opposed to "HBS", which means a hardened steel ball. The "10" is the ball diameter in millimeters. The "3000" is the force in kilograms force.
The hardness may also be shown as XXX HB YYD2. The XXX is the force to apply (in kgf) on a material of type YY (5 for aluminum alloys, 10 for copper alloys, 30 for steels). Thus a typical steel hardness could be written: 250 HB 30D2. It could be a maximum or a minimum.
Typical Hardness Values:
- Softwood (e.g., pine) 1.6 HBS 10/100
- Hardwood 2.6–7.0 HBS 1.6 10/100
- Lead 5.0 HB (pure lead; alloyed lead typically can range from 5.0 HB to values in excess of 22.0 HB)
- Pure Aluminum 15 HB
- Copper 35 HB
- Mild steel 120 HB
- 18–8 (304) stainless steel annealed 200 HB
- Glass 1550 HB
- Hardened tool steel 600–900 HB (HBW 10/3000)
- Rhenium diboride 4600 HB
A convenient conversion fact is that of Brinell hardness to ultimate tensile strength. For quenched and tempered steel, the tensile strength (psi) is about 500 times the Brinell hardness number (provided the strength is not over 200,000 psi).
Related: