Mass Impact Loading Equations
Strength / Mechanics of Materials Table of Content
A mass impacting another object causes deformations that depend on the relative velocity between them. The simplest model for such an event is a mass falling on a spring. The maximum dynamic deformation d of a linearly responding spring is related to the static deformation dst (the deformation caused by a weight W applied slowly) by a factor that depends on h, the height of free fall from a static position.
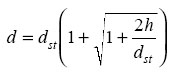
The dynamic and static stresses are related in a similar way,
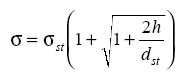
The quantity in parentheses is called the impact factor, which shows the magnification of deflection or stress in impacts involving free fall. Note that the real impact factor is somewhat smaller than what is indicated here, because some energy is always dissipated by friction during the fall and deceleration of the body. This includes internal friction during plastic flow at the points of contact between the bodies. Other small errors may result from neglecting the mass and possible inelasticity of the spring.
A special value of the impact factor is worth remembering. When the load is applied suddenly without
a prior free fall, h = 0, and
![]()
This means that the minimum impact factor is about two, and it is likely to be larger than two, causing perhaps a “bottoming out” of the spring, or permanent damage somewhere in the structure or the payload supported by the spring.