Related Resources: mechanics machines
Power Screw Buckling and Deflection Equations and Calculator
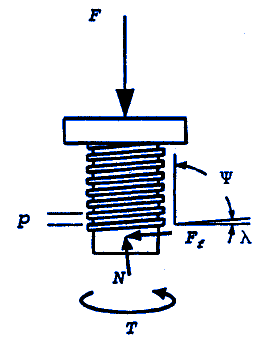
Preview: Power Screw Buckling and Deflection Design Calculator
Power screws subjected to compressive loads may buckle. The Euler formula can be used to estimate the critical load Fc at which buckling will occur for relatively long screws of column length Lc and second moment of area:
I= πd4r / 64
re-written as:
Fc = [( C π2 E ) / L2c ] · I
Second Moment of Inertia:
I = π d4r / 64
Therfore:
Fc = [( C π2 E ) / L2c ] · ( π d4r / 64 )
| Buckling End-Condition Constants | |
| End condition |
C
|
| Fixed-free |
1/4
|
| Rounded-rounded |
1
|
| Fixed-rounded |
2
|
| Fixed-fixed |
4
|
A column of length Lc and radius of gyration k is considered long when its slenderness ratio Lc / k is larger than the critical slenderness ratio:
Lc / k > ( Lc / k )critical
Lc / k > [ ( 2 · π2 C · E ) / Sy ]1/2
The radius of gyration k, cross-sectional area A, and second moment of area I are related by I = A k2, simplifying the above expression to:
Lc / dr > .25 [ ( 2 · π2 · C · E ) / Sy ]1/2
For a steel screw whose yield strength is 60,000 psi and whose end-condition constant is 1.0, the critical slenderness ratio is about 100, and Lc / dr is about 25. For steels whose slenderness ratio is less than critical, the Johnson parabolic relation can be used:
Fc / A = Sy - ( 1 / C · E ) [ ( Sy · Lc ) / ( 2 · π · k ) ]2
which can be solved for a circular cross section of minor diameter dr as:
dr = [ ( fc / ( π Sy ) + ( Sy L2 L2c ) / ( π2 C E ) ]1/2
The load should be externally guided for long travels to prevent eccentric loading. Axial compression or extension δ can be approximated by:
δ = ( F Lc ) / ( A E ) = ( 4 F Lc ) / ( π d4r G )
And similarly, angle of twist Φ, in radians, can be approximated by:
Φ = ( T Lc ) / ( J G ) = ( 32 T Lc ) / ( π d4r G )
Where:
C = Theoretical end-condition constant - see table Buckling End-Condition Constants
E = Modulus of Elasticity (psi)
Lc = Length of Power Screw Column (in)
dr = Root or minor diameter (in)
K = Length Factor
k = Radius of gyration
A = Cross Sectional Area (in2)
Sy = Yield strength (psi)
Fc = Critical Load at Buckling, lbf
Φ = Angle of twist, Radians
G = Shear Modulus, psi
T = Torque Peak, lb-in
J = Polar Second Moment of Inertia, in3
References:
ANSI B1.7M-1984 (R1992), "Screw Threads, Nomenclature, Definitions, and Letter Symbols," American Society of Mechanical Engineers, New York, 1992.
ANSI Bl.5-1977, "Acme Screw Threads," American Society of Mechanical Engineers, New York, 1977.
ANSI Bl.8-1977, "Stub Acme Screw Threads," American Society of Mechanical Engineers, New York, 1977.
ANSI Bl.9-1973 (R1979), "Buttress Screw Threads," American Society of Mechanical Engineers, New York, 1973.