Centripetal Acceleration Equations and Calculator

Centripetal Acceleration, Force Equations and Calculator

Centripetal Acceleration and Force Equations

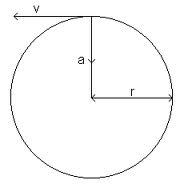
Centripetal Acceleration defines the distance that is covered and the direction of the movement. Since the velocity vector (the direction) of a body changes when moved in a circle - there is an acceleration.

a = v²/ r
r = v² / a
v = (ar)^1/2

Where:

a = Centripetal acceleration and is directed perpendicular to v (m/s², in/s²)
v = Tangential velocity or instantaneous velocity (m/s, ft/s)
r = Radius of the circle (m, ft)
m = meters
ft = feet
s = seconds

Centripetal Force Equations

F = m a
F = m v² / r

Where:

F = centripetal force (N, lb_f)
a = Centripetal acceleration and is directed perpendicular to v (m/s², in/s²)
m = Mass (kg, slugs)
s = seconds

Centripetal Acceleration Calculators
Data Input
Velocity =
Radius =
Result
Centripetal Acceleration =

Data Input
Velocity =
Centripetal Acceleration =
Result
Radius =

Data Input
Centripetal Acceleration =
Radius =
Result
Velocity =

Centripetal Force Calculator
Data Input
Mass =
Centripetal acceleration =
Result
Centripetal Force =

Data Input
Mass =
Velocity =
Radius =
Result
Centripetal Force =

Centrifugal Force Equations and Calculator

Link to this Webpage:

Copy Text to clipboard