Thin Double Convex Lens Optical Equations

Related Resources: physics

Thin Double Convex Lens Optical Equations

Engineering Physics
Engineering and Design Applications

Calculations and Simulations See: Ray Optics Simulation Calculator

As with mirrors, convenient formulas can be used to locate an image mathematically. The derivation of such formulas essentially traces an arbitrary ray geometrically and mathematically from an object point through the two surfaces of a thin lens to the corresponding image point. Snell’s law is applied for the ray at each spherical refracting surface. he details of the derivation involve the geometry of triangles and the approximations mentioned earlier- sin ϕ ≡ Φ, tan ϕ ≡ Φ, and cos ϕ ≡ 1 - to simplify the final results.

Figure 1 shows the essential elements that show up in the final equations, relating object distance p to image distance q, for a lens of focal length f with radii of curvature r₁ and r₂ and refractive index ng. For generality, the lens is shown situated in an arbitrary medium of refractive index n. If the medium is air, then, of course, n = 1.

Figure 1

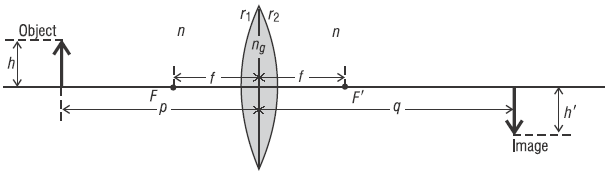
Figure 1 Defining quantities for image formation with a double convex thin lens

Equations for thin lens calculations. The thin lens equation is given by Equation 1.

Equation 1
1 / p + 1 / q = 1 / f

Where:

p = object distance (from object to lens vertex V )
q = image distance (from image to lens vertex V )
f = focal length (from either focal point F or F′ to the lens vertex V )

For a lens of refractive index n_g situated in a medium of refractive index n, the relationship between the parameters n, n_g, r₁, r₂ and the focal length f is given by the lensmaker’s equation:

Equation 2
1 / f = { ( n_g - n ) / n } · { 1 / r₁ - 1 / r₂ }

Where:

n = index of refraction of the surrounding medium,
n_g = index of refraction of the lens materials,
r₁ = radius of curvature of the front face of the lens,
r₂ = radius of curvature of the rear face of the lens.

The magnification m produced by a thin lens is given in Equation:

Equation 3
m = h_i / h_o = - q / p

Where:

m = magnification (ratio of image size to object size)
h_i = transverse size of the image
h_o = transverse size of the object
p and q = object and image distance respectively

Sign convention for thin lens formulas:

Just as for mirrors, we must agree on a sign convention to be used in the application of Equations 1, 2, and 3. It is:

Light travels initially from left to right toward the lens.
Object distance p is positive for real objects located to the left of the lens and negative for virtual objects located to the right of the lens.
Image distance q is positive for real images formed to the right of the lens and negative for virtual images formed to the left of the lens.
The focal length f is positive for a converging lens, negative for a diverging lens.
The radius of curvature r is positive for a convex surface, negative for a concave surface.
Transverse distances (h_o and h_i) are positive above the optical axis, negative below.

References:

Fundamentals of Photonics, Leno S. Pedrottie CORD Waco, Texas