Related Resources: physics
Water Vapor Density
Water Vapor Density atmosphere Equation and proof :
Water vapor in the atmosphere obeys the ideal gas law,
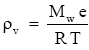
(Eq. 1)
where:
ρv = water vapor density
Mw = molecular weight of water
e = partial pressure of the water vapor
R = universal gas constant
T = air temperature (K).
To be rigorous, we need to recognize that, the partial pressure of dry air is not the barometric pressure P but rather is approximately P – e. That is, in rigorous usage, should be:
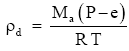
(Eq. 2)
By rearranging (Eq. 1) and (Eq. 2), we can write the following expression for the barometric pressure:
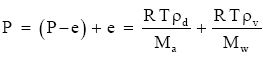
(Eq. 3)
or
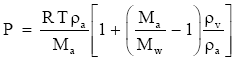
(Eq. 4)
Here,
![]()
(Eq. 5)
is the density of moist air; and we recognize ρv / ρa as the specific humidity, Q
Equation (4) rearranges to
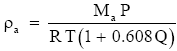
(Eq. 6)
where Ma/Mw − 1 = 0.608. Equation (6) implies that (2.1) is inaccurate by the factor (1 + 0.608Q) if we want the total air density. Since for normal atmospheric conditions Q is seldom larger than 0.035 kg kg-1, the term in parentheses in (6) is always between 1.000 and 1.022. Therefore, (2.1) may be accurate enough for many purposes.
Nevertheless, we often rewrite (Eq. 6) as (e.g., Lumley and Panofsky 1964, p. 214)
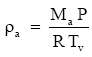
(Eq. 7)
to preserve the form while retaining the accuracy of (Eq. 6) by defining the virtual temperature
![]()
(Eq. 8)
In effect, Tv is the temperature that dry air must have to produce the same density as moist air at the given barometric pressure.
Related: