Related Resources: pressure-vessel
Gas Discharge Rate Atmosphere From a Pressure Vessel
Pressure Vessel Engineering and Design
Fluids Engineering
When a gas is stored under pressure in a closed vessel is discharged to the atmosphere through an orifice, the gas velocity through that orifice may be choked or non-choked. Choked velocity, which is also referred to as sonic velocity, occurs when the ratio of the absolute source pressure to the absolute downstream ambient pressure is equal to or greater than:
[ ( k + 1 ) / 2 ] k / ( k - 1 )
where k is the specific heat ratio of the discharged gas. For many gases, k ranges from about 1.09 to about 1.41, and thus
[ ( k + 1 ) / 2 ] k / ( k - 1 )
ranges from 1.7 to about 1.9. which means that choked velocity usually occurs when the absolute source vessel pressure is at least 1.7 to 1.9 times as high as the absolute ambient atmospheric pressure.
When the gas velocity is choked, the equation for the mass flow rate is:
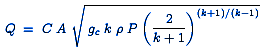
or
![]()
Where the ratio of the absolute source pressure to the absolute downstream ambient pressure is less than [ ( k + 1 ) / 2 ] k / ( k - 1 ) , then the gas velocity is non-choked (i.e., sub-sonic) and the equation for the mass flow rate is:

or
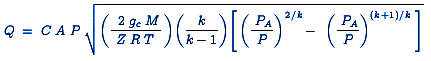
Preview: Discharge Rate Atmosphere From Pressure Vessel Calculator
Where:
| Q | = Mass flow rate, lb / s |
| C | = Discharge coefficient (dimensionless, usually about 0.72) |
| A | = Discharge hole area, ft2 |
| gc | = Gravitational conversion factor of 32.17 ft / s2 |
| k | = cp / cv of the gas = (specific heat at constant pressure) / (specific heat at constant volume) |
| ρ | = Real gas density, lb / ft3 at P and T |
| P | = Absolute source or upstream pressure, lb / ft2 |
| PA | = Absolute ambient or downstream pressure, lb / ft2 |
| M | = Gas molecular weight |
| R | = Universal Gas Law Constant = 1545.3 ft-lb / ( lbmol · °R ) |
| T | = Gas temperature, °R |
| Z | = Gas compressibility factor at P and T (dimensionless) |
The above equations calculate the initial instantaneous flow rate for the pressure and temperature existing in the source vessel when a release first occurs. The initial instantaneous flow rate from a leak in a pressurized gas system or vessel is much higher than the average flow rate during the overall release period because the pressure and flow rate decrease with time as the system or vessel empties. Calculating the flow rate versus time since the initiation of the leak is much more complicated, but more accurate.
The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant R s which only applies to a specific individual gas. The relationship between the two constants is Rs = R / (MW).
Notes:
The above equations are for a real gas.
For an ideal gas, Z = 1 and d is the ideal gas density.
lbmol = pound mole