Related Resources: vibration
Thin Flat Plates Uniform Thickness Natural Frequency Equations and Calculator
Machine Design and Engineering
Thin Flat Plates of Uniform Thickness Natural Frequency Equations and Calculator
ωn = B [ ( E t2 ) / ( ρ a4 ( 1 - v2 )] (1/2)
|
Shape
|
Edge Conditions
|
B Value for Mode
|
|||||||
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
||
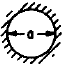 |
Clamped at
Edge |
11.84
|
24.61
|
40.41
|
46.14
|
103.12
|
-
|
-
|
-
|
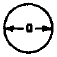 |
Free
|
6.09
|
10.53
|
14.19
|
23.80
|
40.68
|
44.68
|
61.38
|
69.44
|
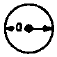 |
Clamped at Center
|
4.35
|
24.26
|
70.39
|
138.85
|
-
|
-
|
-
|
-
|
 |
Simply Supported
at Edge |
5.90
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
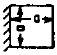 |
One Edge Clamped
Three Edges Free |
1.01
|
2.47
|
6.20
|
7.94
|
9.01
|
-
|
-
|
-
|
 |
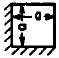
All Edges
Clamped |
10.40
|
21.21
|
31.29
|
38.04
|
38.22
|
47.73
|
-
|
-
|
 |
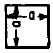
Two Edge Clamped
Two Edges Free |
2.01
|
6.96
|
7.74
|
13.89
|
18.25
|
-
|
-
|
-
|
 |
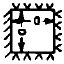
All Edges Free
|
4.07
|
5.94
|
6.91
|
10.39
|
17.80
|
18.28
|
-
|
-
|
 |
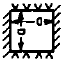
One Edge Clamped
Three Edges Simply Supported |
6.83
|
14.94
|
16.95
|
24.89
|
28.99
|
32.71
|
-
|
-
|
 |
Two Edges Clamped
Two Edges Simply Supported |
8.37
|
15.82
|
20.03
|
27.34
|
29.54
|
37.31
|
-
|
-
|
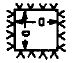 |
All Edges
Simply Supported |
5.70
|
14.26
|
22.82
|
28.82
|
37.08
|
48.49
|
-
|
-
|
Where:
E = Young's Modulus ( lb / in2 ),
t = Thickness of Plate (in),
ρ = Mass Density (lb-sec2 / in4)
a = Diameter of Circular Plate or Side of Square Plate (in),
v = Poisson's Ratio
B = Coefficient for given nodes from image table above,
ωn = Angular Natural Frequency ( rad / sec )
Related and Useful Links:
- Poisson's Ratio
- AISC Steel Construction Shapes Properties Viewer
- Young's Modulus on Common Engineering Materials
Reference Harris, Shock and Vibration Handbook