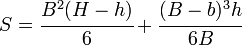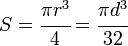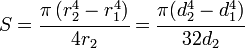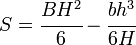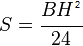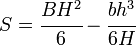Related Resources: material science
Section Modulus Equations and Calculators Common Shapes
Strength of Materials | Beam Deflection and Stress
Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include area for tension, radius of gyration for compression, and moment of inertia for stiffness. Any relationship between these properties is highly dependent on the shape in question. Equations for the section moduli of common shapes are given below. There are two types of section moduli, the elastic section modulus (S) and the plastic section modulus (Z).
For general design, the elastic section modulus is used, applying up to the yield point for most metals and other common materials.
The elastic section modulus is defined as S = I / y, where I is the second moment of area (or moment of inertia) and y is the distance from the neutral axis to any given fiber. It is often reported using y = c, where c is the distance from the neutral axis to the most extreme fiber , as seen in the table below. It is also often used to determine the yield moment (My) such that My = S × σy, where σy is the yield strength of the material.
Extended List of: Section Modulus, Area Moment of Inertia, Equations and Calculators
| Cross section Shape | Equation | Comment |
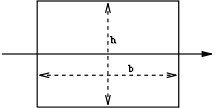 |
Calculator: |
Solid arrow represents neutral axis |
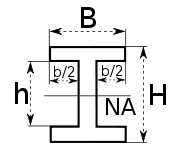 |
Calculator: |
NA indicates neutral axis |
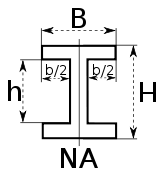 |
Calculator: |
NA indicates neutral axis |
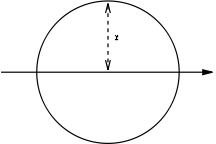 |
Calculator: |
Solid arrow represents neutral axis |
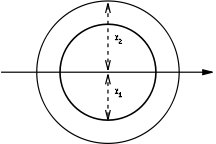 |
Calculator: |
NA indicates neutral axis |
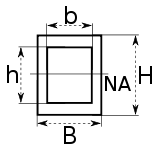 |
Calculator: Section Modulus Hollow Rectangle Square Center Neutral Axis Calculator |
NA indicates neutral axis |
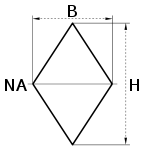 |
Calculator: Section Modulus Diamond Shape Center Neutral Axis Calculator |
NA indicates neutral axis |
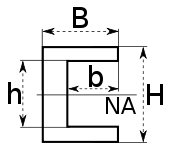 |
Calculator: Section Modulus Channel Shape Center Neutral Axis Calculator |
NA indicates neutral axis |
Plastic Section Modulus (PNA)
The Plastic section modulus is used for materials where (irreversible) plastic behavior is dominant. The majority of designs do not intentionally encounter this behavior.
The plastic section modulus depends on the location of the plastic neutral axis (PNA). The PNA is defined as the axis that splits the cross section such that the compression force from the area in compression equals the tension force from the area in tension. So, for sections with constant yielding stress, the area above and below the PNA will be equal, but for composite sections, this is not necessarily the case.
The plastic section modulus is then the sum of the areas of the cross section on each side of the PNA (which may or may not be equal) multiplied by the distance from the local centroids of the two areas to the PNA:
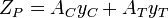
- Section Modulus Equations and Calculators
- Section Properties Radius of Gyration Cases 1 - 10
- Section Properties Radius of Gyration Cases 11 - 16
- Section Properties Radius of Gyration Cases 17 - 22
- Section Properties Radius of Gyration Cases 23 - 27
- Section Properties Radius of Gyration Cases 28 - 31
- Section Properties Radius of Gyration Cases 32 - 34
- Section Properties Radius of Gyration Cases 35 - 37
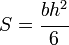
.png)