Mathematics Enclyclopedia
Encyclopedia Menu
Engineering Basic Menu
Engineering Mathematics
Related:
History of Mathematics, Carl Boyer, 735 pages ** Free Membership Minimum Required **
Mathematics is often defined as the study of topics such as quantity, structure, space, and change. Another view, held by many mathematicians, is that mathematics is the body of knowledge justified by deductive reasoning, starting from axioms and definitions. Practical mathematics, in nearly every society, is used for such purposes as accounting, measuring land, or predicting astronomical events. Mathematical discovery or research often involves discovering and cataloging patterns, without regard for application. The remarkable fact that the "purest" mathematics often turns out to have practical applications is what Eugene Wigner has called "the unreasonable effectiveness of mathematics." Today, the natural sciences, engineering, economics, and medicine depend heavily on new mathematical discoveries.The word "mathematics" comes from the Greek (máthema) meaning "science, knowledge, or learning" and (mathematikós) meaning "fond of learning". It is often abbreviated maths in Commonwealth English and math in North American History
The evolution of mathematics might be seen to be an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction was probably that of numbers. The realization that two apples and two oranges do have something in common, namely that they fill the hands of exactly one person, was a breakthrough in human thought. In addition to recognizing how to count concrete objects, prehistoric peoples also recognized how to count abstract quantities, like time -- days, seasons, years. Arithmetic (e.g. addition, subtraction, multiplication and division), naturally followed. Monolithic monuments testify to a knowledge of geometry. Further steps need writing or some other system for recording numbers such as tallies or the knotted strings called khipu used by the Inca empire to store numerical data. Numeral systems have been many and diverse. Historically the major disciplines within mathematics arose, from the start of recorded history, out of the need to do calculations on taxation and commerce, to understand the relationships among numbers, to measure land, and to predict astronomical events. These needs can be roughly related to the broad subdivision of mathematics, into the studies of quantity, structure, space, and change. Mathematics since has been much extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries have been made throughout history and continue to be made today. Inspiration pure and applied mathematics, and aesthetics. Mathematics arises wherever there are difficult problems that involve quantity, structure, space, or change. At first these were found in commerce, land measurement and later astronomy; nowadays, all sciences suggest problems studied by mathematicians, and many problems arise within mathematics itself. Newton invented infinitesimal calculus and Feynman his Feynman path integral using a combination of reasoning and physical insight, and today's string theory also inspires new mathematics. Some mathematics is only relevant in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts.As in most areas of study, the explosion of knowledge in the scientific age has led to specialization in mathematics. One major distinction is between pure mathematics and applied mathematics. Within applied mathematics, two major areas have split off and become disciplines in their own right, statistics and computer science.Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty also in a numerical method that speeds calculation, such as the fast Fourier transform. G. H. Hardy in "A Mathematicians Apology" expressed the belief that these esthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. Notation language, and rigor
Mathematical writing is not easily accessible to the layperson. A Brief History of Time, Stephen Hawking's 1988 bestseller, contained a single mathematical equation. This was the author's compromise with the publisher's advice, that each equation would halve the sales.The reasons for the inaccessibility even of carefully-expressed mathematics can be partially explained. Contemporary mathematicians strive to be as clear as possible in the things they say and especially in the things they write (this they have in common with lawyers). They refer to rigor. To accomplish rigor, mathematicians have extended natural language. There is precisely-defined vocabulary for referring to mathematical objects, and stating certain common relations. There is an accompanying mathematical notation, which like musical notation has a definite content, and also has a strict grammar (under the influence of computer science, more often now called syntax). Some of the terms used in mathematics are also common outside mathematics, such as ring, group and category; but are not such that one can infer the meanings. Some are specific to mathematics, such as homotopy and Hilbert space. It was said that Henri Poincaré was only elected to the Académie Française so that he could tell them how to define automorphe in their dictionary. Rigoris fundamentally a matter of mathematical proof. Mathematicians want their theorems to follow mechanically from axioms by means of formal axiomatic reasoning. This is to avoid mistaken 'theorems', based on fallible intuitions; of which plenty of examples have occurred in the history of the subject (for example, in mathematical analysis).Axioms in traditional thought were 'self-evident truths', but that conception turns out not to be workable in pushing the mathematical boundaries. At a formal level, an axiom is just a string of symbols, which has an intrinsic meaning only in the context of all derivable formulas of an axiomatic system. It was the goal of Hilbert's program to put all of mathematics on a firm axiomatic basis, but according to Gödel's incompleteness theorem every (strong enough) axiom system has un decidable formulas; and so a final axiomatization of mathematics is unavailable. Nonetheless mathematics is often imagined to be (as far as its formal content) nothing but set theory in some axiomatization, in the sense that every mathematical statement or proof could be cast into formulas within set theory.Is mathematics a science?Carl Friedrich Gauss referred to mathematics as the Queen of the Sciences. The mathematician-physicist Leon M. Lederman has quipped: "The physicists defer only to mathematicians, and the mathematicians defer only to God (though you may be hard pressed to find a mathematician that modest)."If one considers science to be strictly about the physical world, then mathematics, or at least pure mathematics, is not a science. An alternative view is that certain scientific fields (such as theoretical physics) are mathematics with axioms that are intended to correspond to reality. In fact, the theoretical physicist, J. M. Ziman, proposed that science is public knowledge and thus includes mathematics.
In any case, mathematics shares much in common with many fields in the physical sciences, notably the exploration of the logical consequences of assumptions. Intuition and experimentation also play a role in the formulation of conjectures in both mathematics and the (other) sciences. Overviewof fields of mathematics As noted above, the major disciplines within mathematics first arose out of the need to do calculations in commerce, to understand the relationships between numbers, to measure land, and to predict astronomical events. These four needs can be roughly related to the broad subdivision of mathematics into the study of quantity, structure, space, and change (i.e. arithmetic, algebra, geometry and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations) and to the empirical mathematics of the various sciences (applied mathematics).The study of quantity starts with numbers, first the familiar natural numbers and integers and their arithmetical operations, which are characterized in arithmetic. The deeper properties of whole numbers are studied in number theory.The study of structure began with investigations of Pythagorean triples. Neolithic monuments on the British Isles are constructed using Pythagorean triples. Eventually, this led to the invention of more abstract numbers, such as the square root of two. The deeper structural properties of numbers are studied in abstract algebra and the investigation of groups, rings, fields and other abstract number systems. Included is the important concept of vectors, generalized to vector spaces and studied in linear algebra. The study of vectors combines three of the fundamental areas of mathematics, quantity, structure, and space.The study of space originates with geometry, beginning with Euclidean geometry. Trigonometry combines space and number. The modern study of space generalizes these ideas to include higher-dimensional geometry, non-Euclidean geometries (which play a central role in general relativity) and topology. Quantity and space both play a role in analytic geometry, differential geometry, and algebraic geometry. Within differential geometry are the concepts of fiber bundles, calculus on manifolds. Within algebraic geometry is the description of geometric objects as solution sets of polynomialequations, combining the concepts of quantity and space, and also the study of topological groups, which combine structure and space. Lie groups are used to study space, structure, and change. Topology in all its many ramifications may be the greatest growth area in 20th century mathematics. Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a most useful tool. The central concept used to describe a changing quantity is that of a function. Many problems lead quite naturally to relations between a quantity and its rate of change, and the methods of differential equations. The numbers used to represent continuous quantities are the real numbers, and the detailed study of their properties and the properties of real-valued functions is known as real analysis. These have been generalized, with the inclusion of the square root of negative one, to the complex numbers, which are studied in complex analysis. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many phenomena in nature can be described by dynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet still deterministic behavior. Beyond quantity, structure, space, and change are areas of pure mathematics that can be approached only by deductive reasoning. In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic, which divides into recursion theory, model theory, and proof theory, is now closely linked to computer science.
When electronic computers were first conceived, several essential theoretical concepts in computer science were shaped by mathematicians, leading to the fields of computability theory, computational complexity theory, and information theory. Many of those topics are now investigated in theoretical computer science. Discrete mathematics is the common name for the fields of mathematics most generally useful in computer science.An important field in applied mathematics is statistics, which uses probability theory as a tool and allows the description, analysis, and prediction of phenomena where chance plays a part. It is used in all the sciences. Numerical analysis investigates methods for using computers to efficiently solve a broad range of mathematical problems that are typically beyond human capacity, and taking rounding errors or other sources of error into account to obtain credible answers.
Major themes in mathematics:
 |
|---|
| Natural numbers |
 |
|---|
| Integers |
 |
|---|
| Rational numbers |
 |
|---|
| Real numbers |
 |
|---|
| Complex numbers |
Structure
Pinning down ideas of size, symmetry, and mathematical structure.
-



Abstract algebra Number theory Group theory 


Topology Category theory Order theory
Space
A more visual approach to mathematics.
-

Topology Geometry Trigonometry
 |
|
| Differential geometry | Fractal geometry |
Change
Ways to express and handle change in mathematical functions, and changes between numbers.
-
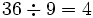

Arithmetic Calculus 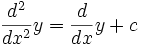

Differential equations Dynamical systems
 |
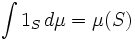 |
| Vector calculus | Analysis |
 |
|
| Chaos theory |
Discrete mathematics
Discrete mathematics involves techniques that apply to objects that can only take on specific, separated values.
-
[1,2,3][1,3,2]
[2,1,3][2,3,1]
[3,1,2][3,2,1]

Combinatorics Naive set theory Theory of computation
 |
 |
| Cryptography | Graph theory |
Common misconceptions:
Mathematics is not a closed intellectual system, in which everything has already been worked out. There is no shortage of open problems. Pseudo mathematics is a form of mathematics-like activity undertaken outside academia, and occasionally by mathematicians themselves. It often consists of determined attacks on famous questions, consisting of proof-attempts made in an isolated way (that is, long papers not supported by previously published theory). The relationship to generally-accepted mathematics is similar to that between pseudo science and real science. The misconceptions involved are normally based on:
-
misunderstanding of the implications of mathematical rigor;
-
attempts to circumvent the usual criteria for publication of mathematical papers in a learned journal after peer review, with assumptions of bias;
-
lack of familiarity with, and therefore underestimation of, the existing literature.
The case of Kurt Heegner's work shows that the mathematical establishment is neither infallible, nor unwilling to admit error in assessing 'amateur' work. And like astronomy, mathematics owes much to amateur contributors such as Fermat and Mersenne. Mathematics is not accountancy. Although arithmetic computation is crucial to accountants, their main concern is to verify that computations are correct through a system of double checks. Advances in abstract mathematics are mostly irrelevant to the efficiency of concrete bookkeeping, but the use of computers clearly does matter. Mathematics is not numerology. Numerology uses modular arithmetic to reduce names and dates down to numbers, but assigns emotions or traits to these numbers intuitively or on the basis of traditions .
Mathematical concepts and theorems need not correspond to anything in the physical world. In the case of geometry, for example, it is not relevant to mathematics to know whether points and lines exist in any physical sense, as geometry starts from axioms and postulates about abstract entities called "points" and "lines" that we feed into the system. While these axioms are derived from our perceptions and experience, they are not dependent on them. And yet, mathematics is extremely useful for solving real-world problems. It is this fact that led Eugene Wigner to write an essay on The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Mathematics is not about unrestricted theorem proving, any more than literature is about the construction of grammatically correct sentences. However, theorems are elements of formal theories, and in some cases computers can generate proofs of these theorems more or less automatically, by means of automated theorem provers. These techniques have proven useful in formal verification of programs and hardware designs. However, they are unlikely to generate (in the near term, at least) mathematics with any widely recognized aesthetic value.