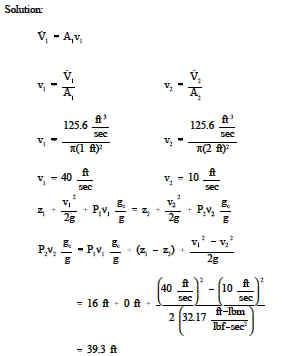|
|
|
|
Energy
Conversions in Fluid Systems - Fluid Flow
|
|
|
|
|
Fluid
Flow Table of Contents
Bernoulli’s equation makes it easy to examine how energy
transfers take place among elevation head,
velocity head, and pressure head. It is possible to examine individual
components of piping systems and determine
what fluid properties are varying and how the energy balance is affected.
If a pipe containing an ideal fluid undergoes a gradual
expansion in diameter, the continuity equation
tells us that as the diameter and flow area get bigger, the flow velocity must
decrease to maintain the same mass flow
rate. Since the outlet velocity is less than the inlet velocity, the velocity
head of the flow must decrease from the inlet to the outlet. If the pipe lies
horizontal, there is no change in elevation
head; therefore, the decrease in velocity head must be compensated
for by an increase in pressure head. Since we are considering an ideal fluid
that is incompressible, the specific volume
of the fluid will not change. The only way that the pressure
head for an incompressible fluid can increase is for the pressure to increase.
So the Bernoulli equation indicates that a
decrease in flow velocity in a horizontal pipe will result in an increase
in pressure.
If a constant diameter pipe containing an ideal fluid undergoes
a decrease in elevation, the same net effect
results, but for different reasons. In this case the flow velocity and the
velocity head must be constant to satisfy
the mass continuity equation.
So the decrease in elevation head can only be compensated for by
an increase in pressure head. Again, the
fluid is incompressible so the increase in pressure head must result in an
increase in pressure.
Although the Bernoulli equation has several restrictions placed
upon it, there are many physical fluid
problems to which it is applied. As in the case of the conservation of mass, the
Bernoulli equation may be applied to
problems in which more than one flow may enter or leave the system at
the same time. Of particular note is the fact that series and parallel piping
system problems are solved using the
Bernoulli equation.
|
|
|
