Related Resources: vibration
Natural Frequency Three Masses Equations and Calculator
Machine Design and Engineering
Angular Natural Frequency Three Masses Axial Equations and Calculator
Mass Spring Systems in Translation Equation and Calculator
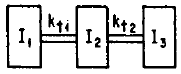
ωn = { (1/2) [ B ± ( B2 - (( 4 kt1kt2 ) / ( I1 I2 I3 )) ( I1 + I2 + I3) ) (1/2) ] }(1/2)
or
ωn+ = { (1/2) [ B + ( B2 - (( 4 kt1kt2 ) / ( I1 I2 I3 )) ( I1 + I2 + I3) ) (1/2) ] }(1/2)
ωn- = { (1/2) [ B - ( B2 - (( 4 kt1kt2 ) / ( I1 I2 I3 )) ( I1 + I2 + I3) ) (1/2) ] }(1/2)
and
B = kt1/ I1 + kt2/ I3 + ( kt1 + kt2 ) / I2
Where:
kt1, t2 = Torsional Stiffness of Shaft ( lb-in/rad )
I1, 2 = Rotary Mass Moment of Inertia of Mass ( lb-in-sec2 )
ωn+, n- = Angular Natural Frequency ( rad/sec )
Reference Harris, Shock and Vibration Handbook