Related Resources: vibration

Simple harmonic force rotary unbalance

Vibration Design Formulas and Calculators
Spring Design and Engineering, Formulas

Forced damped vibration - A simple harmonic force applied to mass due to rotary unbalance vibration Equations

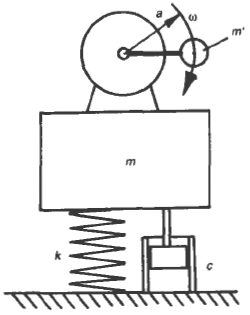
F = m_r·a·ω²·cos ( ω · t )
(due to mass m_r, rotating at radius a angular velocity ω)

The amplitude varies with frequency as follows:

Q = - r² / [ ( 1 - r² )² + 4 R² r² ) ]^0.5

α = tan^-1 ( 2 R r ) / ( 1 - r² )

Where:

R = ω_c / ω_n

and

r = ω / ω_n

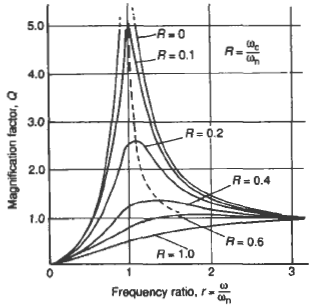
Frequency ratio to Magnification factor ratio chart

r = Frequency ratio,
R = Damping ratio,
ω_c = Critical frequency = c / ( 2 m )
ω_n = spring mass system = ( k / m )^0.5

1 rad/sec = 1/( 2π ) Hz

Related and Useful Links:

• Harmonic Force Constant Amplitude Applied To Base Vibration Equations
• Harmonic Force of Constant Amplitude Applied to Mass in Vibration Equations
• Shock and Vibration Response Equations
• Vibration Severity Chart

Reference: Mechanical Engineers Data Handbook, J. Carvill 1993