Related Resources: calculators

Circular Membrane Stress and Deflection Calculator and Equations

Flat Plates Stress, Deflection Design Equations and Calculators

Circular Membrane Stress and Deflection Design Calculator and Equations

A membrane may be defined as a plate that is so thin that it may ne considered to have no bending rigidity. The only stresses present are in the plane of the surface and are uniform throughout the thickness of the membrane.

Preview: Circular Membrane Stress and Deflection Design Calculator

Figure 1 shows two views of a circular membrane with the edge clamped under a uniform pressure, p.

The maximum deflection of this membrane is at the center and is given by

Eq. 1

${\displaystyle {\mathrm{\delta <!--\; \delta \; -->}}_c=0.662R\sqrt[3]{\frac{pR}{Et}}}$

The deflection of the membrane at a distance, r, from the center is

${\displaystyle \mathrm{\delta <!--\; \delta \; -->}={\mathrm{\delta <!--\; \delta \; -->}}_c[1-<!--\; -\; -->0.09{\left(\frac{r}{R}\right)}^2-<!--\; -\; -->0.1{\left(\frac{r}{R}\right)}^5]}$

The stress at the center of this membrane is

${\displaystyle f=0.423\sqrt[3]{\frac{E{p}^2{R}^2}{t^2}}}$

while that at the edge is

${\displaystyle f_e=0.328\sqrt[3]{\frac{E{p}^2{R}^2}{t^2}}}$

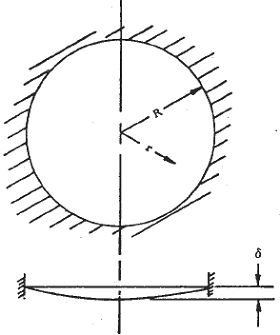
Figure 1, Circular Membrane with Clamped Edge

Where

p = pressure
f = calculated stress
E = modulus of elasticity
r = cylindrical coordinate
R = outside radius of circular membrane
t = thickness of membrane
δ = deflection
δ_c = center deflection of circular membrane
f = stress at center
f_e = stress at edge

• Bell Helicopter Structural Design Manual, 1977

Related

• Circular Plate Concentrated Load Edges Fixed Support Equation and Calculator Circular Plate Concentrated Load Edges fixed Supported Equation and Calculator
• Circular Plate Concentrated Load Floating Equation and Calculator Circular Plate Concentrated Load Floating Equation and Calculator
• Circular plate, uniform load, edges clamped equation and calculator Circular flat plates subject to concentrated or distributed loads (pressure) with the edge either clamped or supported.
• Circular plate, uniform load, edges simply supported equation and calculator Maximum stress and deflection for circular flat plates subject to concentrated or distributed loads (pressure) with the edge either clamped or supported.
• Concentrated load at center of Plate, clamped edges (empirical) equation and calculator
• Rectangular plate, concentrated load at center, simply supported (empirical) equation and calculator
• Bending of Circular Sandwich Plate by Load Applied Through an Insert
• Design Thickness of Pipe Blanks Caps Formula and Calculator per. ASME B31.5
• Regular polygonal plate; all edges simply supported with uniform loading over entire plate Stress and Deflection Equation and Calculator . Per. Roarks Formulas for Stress and Strain
• Regular polygonal plate; all edges fixed with uniform loading over entire plate Stress and Deflection Equation and Calculator . Per. Roarks Formulas for Stress and Strain
• Continuous Plate Supported on an Elastic Foundation of Modulus k (lb/in 2 /in) Stress and Deflection Equation and Calculator . Uniform loading over a small circle of radius r o , adjacent to edge but remote from corner. Per. Roarks Formulas for Stress and Strain
• Combined Stress Circular Cantilever Beam in Direct Compression and Beam Deflection Calculator
• Combined Stress Circular Cantilever Beam in Direct Tension and Stress Deflection Calculator
• Combined Rectangular Cantilever Beam in Direct Compression Equations and Beam Deflection Calculator
• Combined Rectangular Cantilever Beam in Direct Tension and Deflection Equations and Calculator
• Combined Loading on Circular Beam or Shaft in Direct Compression and Deflection Equation and Calculator
• Combined Loading on Circular Beam or Shaft in Direct Tension and Deflection Equation and Calculator
• Combined Loading on Rectangular Beam or Shaft in Direct Compression and Deflection Equation and Calculator
• Combined Loading on Rectangular Beam or Shaft in Direct Tension and Deflection Equation and Calculator
• Combined Loading on Circular Shaft in Direct Compression and Torsion Equation and Deflection Calculator