Civil Engineering & Design

RECTANGULAR CONCRETE BEAM/SECTION ANALYSIS Flexure, Shear, Crack Control, and Inertia for Singly or Doubly Reinforced Sections Per ACI 318-05 Code Hover Curser over Results Value to See Notes Input Data: 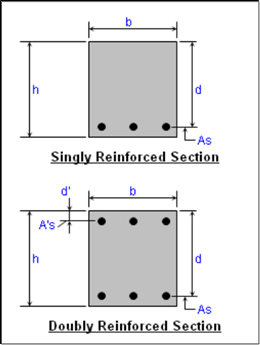Beam or Slab Section? Beam Slab Exterior or Interior Exposure? Exterior Interior Reinforcing Yield Strength, fy = ksi Concrete Comp. Strength, f 'c = ksi in. Depth to Tension Reinforcing, d = in. in. Tension Reinforcing, As = in.^2 Tension Reinf. Bar Spacing, s1 = in. Clear Cover to Tension Reinf., Cc = in. Depth to Compression Reinf., d' = in. Compression Reinforcing, A's = in.^2 Working Stress Moment, Ma = ft-kips Ultimate Design Moment, Mu = ft-kips Ultimate Design Shear, Vu = kips Total Stirrup Area, Av(stirrup) = in.^2 Tie/Stirrup Spacing, s2 = in. Results: Crack Control (Distribution of Reinf.): b1 = The factor, 'b1', shall be = 0.85 for concrete strengths (f'c) <= 4000 psi. For concrete strengths > 4,000 psi, 'b1' shal be reduced continuously at a rate of 0.05 for each 1000 psi of strength > 4000 psi, but 'b1' shall not be taken < 0.65. ?? Per ACI 318-05 Code: c = The value, 'c', is the distance from the compression face of the beam/section to the neutral axis, and is calculated as follows: For Singly Reinforced Beam/Section: c = (As*fy/(0.85*f'c*b))/b1 For Doubly Reinforced Beam/Section: c = (Asmax*fy/(0.85*f'c*b))/b1 in. Es = The Modulus of Elasticity for Steel, 'Es', is assumed = 29,000 ksi ksi a = The value, 'a', is the depth of the assumed retangular compression stress block, and is calculated as follows: a = c*b1 in. Ec = The Modulus of Elasticity for Concrete, 'Ec', is calculated as follows: Ec = 57*(f'c*1000)^(1/2) ksi Note: "normal" weight concrete is assumed. ksi rb =?? The Reinforcing Ratio, 'rb', is the reinforcing ratio producing balanced strain conditions and is calculated as follows: rb = 0.85*b1*f'c/fy*(87/(87+fy)) n = The Modular Ratio, 'n', is calculated as follows: n = Es/Ec n = Es/Ec r(prov) =?? The Ratio of Tension Reinforcing provided, 'r', is calculated as follows: r = As/(b*d) fs = The working stress tension in the reinforcing, 'fs', is calculated as follows: fs = 12*Ma/(n*As*d*(1-((2*As/b*d)+(n*As/(b*d))^2)^(1/2)-n*As/(b*d))/3)) ksi r(min) =?? The minimum required percentage of flexural reinforcing, 'r(min)', is calculated as follows: r(min) >= 3*(f'c)^(1/2)/fy >= 200/fy where: f'c and fy are in psi. fs(used) = The actual value of 'fs' used in the calculation of the required spacing of flexural tension reinforcing shall be the lesser of the calculated value of 'fs' based on the applied moment and 2/3*fy. ksi As(min) = The minimum required area of flexural reinforcing, 'As(min)', is calculated as follows: As(min) = r(min)*b*d s1(max) = The center-to-center spacing, 's', of the flexural tension reinforcing shall not exceed the following: s1(max) = 15*(40/fs)-2.5*Cc but not greater than 12*(40/fs). r(temp) =?? The minimum required percentage of temperature reinforcing, 'r(temp)', is calculated as follows: r(temp) = 0.0020 for fy = 40 and 50 ksi r(temp) = 0.0018 for fy = 60 ksi r(temp) = 0.0018*60/fy for fy > 60 ksi Note: minimum temperature reinforcing percentage is not used for beams, only slab sections. (total for section) As(temp) = The minimum required area of temperature reinforcing, 'As(temp)', is calculated as follows: As(temp) = r(temp)/2*b*h Note: 1/2 of the entire percentage, r(temp), is used in each face of section. ?? Per ACI 318-95 Code: r(max) =?? The Reinforcing Ratio, 'r(max)', is the maximum allowable reinforcing ratio and is calculated as follows: For Singly Reinforced Beam/Section: r(max) = 0.75*rb For Doubly Reinforced Beam/Section: r(max) = 0.75*rb+r '*f'sb/fy where: r ' = A's/(b/d) f'sb = 87*(1-d'/d)*(87+fy)/87 <= fy dc = The concrete cover, 'dc', is the distance from the tension face of the beam/section to the centerline of the tension reinforcing and is calculated as follows: dc = h-d in. As(max) = The maximum allowable area of reinforcing, 'As(max)', is calculated as follows: For Singly Reinforced Beam/Section: As(max) = 0.75*rb*b*d For Doubly Reinforced Beam/Section: As(max) = (0.75*rb+r '*f'sb/fy)*b*d z = The factor limiting the distribution of flexural reinforcement, 'z', is calculated as follows: z = fs*(dc*2*dc*b/Nb)^(1/3) k/in. f 's = z(allow) = The allowable factor limiting the distribution of flexural reinforcement, 'z(allow)', shall not exceed the following values: Interior Exposure: Exterior Exposure: Beams z = 175 z = 145 One-way slabs z = 156 z =129 fMn = The Ultimate Moment Capacity, 'fMn', of the beam/section is calculated as follows: For Singly Reinforced Beam/Section: fMn = f*(0.85*f'c*a*b*(d-a/2)) For Doubly Reinforced Beam/Section: fMn = f*(0.85*f'c*a*b*(d-a/2)+A's*f's*(d-d')) where: f = 0.9 f's = (1-d'/c)*87 <= fy Moment of Inertia for Deflection: fVc = The ultimate shear strength provided by the concrete, 'fVc', is calculated as follows: For shear and flexure only (no axial load): fVc = 2*f*(f'c*1000)^(1/2)*b*d For shear with axial compression: fVc = 2*f*(1+Pu/(2*Ag)*(f'c*1000)^(1/2)*b*d For shear with axial tension: fVc = 2*f*(1+Pu/(0.5*Ag)*(f'c*1000)^(1/2)*b*d where: f = 0.75 Ag = b*h Note: for members such as one-way slabs, footings, and walls, where minimum shear reinforcing is not required, if fVc >= Vu then the section is considered adequate. For beams, when Vu > fVc/2 , then a minimum area of shear reinforcement is required. fr = The Modulus of Rupture of concrete, 'fr', is calculated as follows: fr = 7.5*(f'c*1000)^(1/2) ksi ksi fVs = The ultimate shear strength provided by the shear reinforcing in beams, 'fVs', is calculated as follows: fVs = f*fy*d*Av/s2 where: f = 0.75 The required amount of shear strength to be provided by the shear reinforcing in beams is: fVs(req'd) = Vu-fVc >= 0. The required amount of shear strength to be provided must be <= fVs(max). kips kd = The distance from the compression face of the beam/section to the neutral axis, 'kd', is calculated as follows: for singly reinforced beams/sections: kd = ((2*d*B+1)^(1/2)-1)/B where: Es = 29000 ksi (for reinforcing steel) Ec = 57*(f'c*1000)^(1/2) ksi (for normal weight concrete) n = Es/Ec B= b/(n*As) for doubly reinforced beams/sections: kd = ((2*d*B*(1+r*d'/d+(1+r)^2)^(1/2)-(1+r))/B where: B = b/(n*As) r = (n-1)*A's/(n*As) in. fVn = fVc+fVs = Ig = The Gross (uncracked) Moment of Inertia, 'Ig', is calculated as follows: Ig = b*h^3/12 in.^4 fVs(max) = The maximum allowable ultimate shear strength to be provided by the shear reinforcing in beams, 'fVs(max)', is calculated as follows: fVs(max) <= 8*f*(f'c*1000)^(1/2)*b*d/1000 where: f = 0.75 Mcr = The Cracking Moment, 'Mcr', is calculated as follows: Mcr = fr*Ig/yt where: yt = h/2 ft-k Av(prov) = in.^2?? = Av(stirrup) Icr = The Cracked Section Moment of Inertia, 'Icr', is calculated as follows: for singly reinforced: Icr = b*kd^3/3+n*As*(d-kd)^2 for doubly reinforced: Icr = b*kd^3/3+n*As*(d-kd)^2+(n-1)*A's*(kd-d')^2 in.^4 Av(req'd) = The required area of shear reinforcing, 'Av', perpendicular to axis of the beam is calculated as follows: Av = fVs*s2/(f*fy*d) >= Av(min) where: f = 0.75 fVs = max. of: (Vu - fVc) or 0 Note: Av = area of both legs of a closed tie or stirrup. Ie = The Effective Moment of Inertia, 'Ie', is calculated as follows: Ie = (Mcr/Ma)^3*Ig+(1-(Mcr/Ma)^3)*Icr <= Ig in.^4?? (for deflection) Av(min) = The minimum area of shear reinforcing, 'Av(min)', to be provided for beams is calculated as follows: Av(min) = 75*SQRT(f'c*1000)*b*s2/fy but not less than: 50*b*s2/(fy*1000) Note: Av(min) = area of both legs of a closed stirrup. s2(max) = The maximum allowable shear reinforcing (closed stirrup) spacing, 's2', shall not exceed d/2, nor 24". However, when fVs > 4*f*(f'c*1000)^(1/2)*b*d, then the maximum spacing given above shall be reduced by one-half. (Note: f = 0.75) c = The value, 'c', is the distance from the compression face of the beam/section to the neutral axis, and is calculated as follows: For Singly Reinforced Beam/Section: c = (As*fy/(0.85*f'c*b))/b1 For Doubly Reinforced Beam/Section: c = (Asmax*fy/(0.85*f'c*b))/b1 in. a = The value, 'a', is the depth of the assumed retangular compression stress block, and is calculated as follows: a = c*b1 in. r =?? The Ratio of Tension Reinforcing, 'r', is calculated as follows: For Singly Reinforced Beam/Section: r = As/(b*d) r = (f*fy-((f*fy)^2-4*(f*0.59*fy^2/f'c)*(12*Mu/b*d^2))^(1/2))/(2*(f*0.59*fy^2/f'c)) where: f = 0.9 For Doubly Reinforced Beam/Section: If A's yields, where f's = (1-d'/c)*87 >= fy , then r =(0.75*rb)+(A's/(b*d)) If A's does not yield, where f's = (1-d'/c)*87 < fy , then r = (0.75*rb)+(A's/(b*d))*(f's/fy) As = The area of required tension reinforcing, 'As', is calculated as follows: For Singly Reinforced Beam/Section: As = r*b*d For Doubly Reinforced Beam/Section: If A's yields, where f's = (1-d'/c)*87 >= fy , then As = (0.75*rb*b*d)+(Mu/f-0.85*f'c*a*b*(d-a/2))/(fy*(d-d')) If A's does not yield, where f's = (1-d'/c)*87 < fy , then As = (0.75*rb*b*d)+((Mu/f-0.85*f'c*a*b*(d-a/2))/(fy*(d-d')))*(f's/fy) where: f = 0.9 in.^2 (4/3)*As = in.^2 f 's = For the case of a doubly reinforced beam/section only, the compression stress in the compression reinforcing, 'f's', is calculated as follows: If f's yields, where (1-d'/c)*87 >= fy , then f's = fy If f's does not yield, then f's = (1-d'/c)*87 < fy ksi A's = For the case of a doubly reinforced beam/section only, the area of required compression reinforcing, 'A's', is calculated as follows: If A's yields, where f's = (1-d'/c)*87 >= fy , then A's = (Mu/f-0.85*f'c*a*b*(d-a/2))/(fy*(d-d')) If A's does not yield, where f's = (1-d'/c)*87 < fy , then As = ((Mu/f-0.85*f'c*a*b*(d-a/2))/(fy*(d-d')))*(f's/fy) where: f = 0.9 in.^2 The required area of flexural reinforcing to be used, 'As(use)', for singly reinforced beam-type sections is calculated as follows: If As < As(min) then As(use) = lesser of r(min)*b*d or (4/3)*r*b*d , otherwise As(use) = As. The required area of flexural reinforcing to be used, 'As(use)', for singly reinforced slab-type sections is calculated as follows: If As < As(temp) then As(use) = r(temp)/2*b*h (per face) , otherwise As(use) = As. Update Reset Print Link to this Webpage: Copy Text to clipboard Click for Suggested Citation © Copyright 2000 - 2024, by Engineers Edge, LLC www.engineersedge.com All rights reserved Disclaimer | Feedback Advertising | Contact Privacy Policy

Home
Engineering Book Store
Engineering Forum
Applications and Design
Beam Deflections and Stress
Bearing Apps, Specs & Data
Belt Design Data Calcs
Civil Engineering
Design & Manufacturability
Electric Motor Alternators
Engineering Calculators
Excel App. Downloads
Flat Plate Stress Calcs
Fluids Flow Engineering
Friction Engineering
Gears Design Engineering
General Design Engineering
Hardware, Imperial, Inch
Hardware, Metric, ISO
Heat Transfer
Hydraulics Pneumatics
HVAC Systems Calcs
Economics Engineering
Electronics Instrumentation
Engineering Mathematics
Engineering Standards
Finishing and Plating
Friction Formulas Apps
Lubrication Data Apps
Machine Design Apps
Manufacturing Processes
Materials and Specifications
Mechanical Tolerances Specs
Plastics Synthetics
Power Transmission Tech.
Pressure Vessel
Pumps Applications
Re-Bar Shapes Apps
Section Properties Apps
Strength of Materials
Spring Design Apps
Structural Shapes
Threads & Torque Calcs
Thermodynamics
Physics
Vibration Engineering
Videos Design Manufacture
Volume of Solids Calculators
Welding Stress Calculations
Training Online Engineering

Copyright Notice