Related Resources: pressure-vessel

Spherical Cylinder Stress and Deflection Own weight Formula and Calculator

Spherical Cylinder Stress and Deflection Own weight, δ force/unit volume; tangential top edge support Equation and Calculator.

Per. Roarks Formulas for Stress and Strain for membrane stresses and deformations in thin-walled pressure vessels.

Preview: Spherical Cylinder Stress and Deflection Internal or External Pressure Calculator

Spherical Cylinder Stress and Deflection

Own weight, δ force/unit volume; tangential top edge support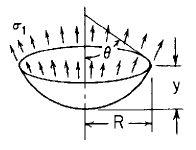

Deflection and Stress Own weight, δ force/unit volume; tangential top edge support.

For R₂ / t > 10

Meridional Stress

Circumferential Hoop Stress

Maximum tensile stress

		at θ = 0°

 

σ2 = 0

at θ = 51.83°

 

Radial Displacement of Circumference

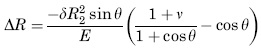
Change in height dimension y

Rotation of a meridian from its unloaded position

Where used:
E = Modulus of Elasticity (lbs/in²)
v = Poisson's ratio
δ = Density (lbs/in³)
σ_1,2 = Stress, (lbs/in²)
R₂ = Radius (in)
R = Distance as indicated (in)
y = Depth as indicated (in), Must be equal too or less than d
d = Depth of liquid (in)
t = Wall thickness (in)
θ = Angle (deg.)
ψ = Rotation of a meridian from its unloaded position, positive when that meridional rotation represents an increase in ΔR when y or θ increases;

(Note: There is a discontinuity in the rate of increase in fluid pressure at the top of the liquid. This leads to some bending in this region and is indicated by a discrepancy in the two expressions for the meridional slope at y = d.)

Reference:

Roarks Formulas for Stress and Strain, 7th Edition