Calculator for Beam Deflection and Stress Equations Calculator for Beam Supported on Both Ends Loaded Two equal Loads

Beam Deflection and Stress Formula and Calculators

Area Moment of Inertia Equations & Calculators

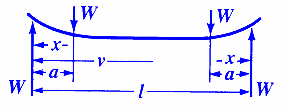
Structural Beam Deflection, Stress, Bending Equations and calculator for a Beam Supported on Both Ends Loaded Two equal Loads.

Open
Stress and Deflection Beam Supported Both Ends Loaded Two Equal Loads Calculator

---

Beam Stress between nearest load and support point

Beam Stress between the two loads

---

Beam Stress at each load application and all points between

---

Beam Deflection between nearest load and support point

Beam Deflection between loads

---

Maximum Beam Deflection at Center

Beam Deflection at loads

---

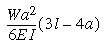
Where:

E =	Modulus of Elasticity	psi	(N/mm2)
I =	Moment of Inertia	in4	(mm4)
W =	Load on Beam	lbs	(N)
s =	Stress at the cross-section being evaluated	Lbs/in2	(N/mm2)
y =	Beam Deflection (Positive Upward Beam Deflection, Negative Downward	inches	(mm)
x =	Some distance as indicated	inches	(mm)
a =	Some distance as indicated	inches	(mm)
v =	Some distance as indicated	inches	(mm)
l =	Some distance as indicated	inches	(mm)
Z =	section modulus of the cross-section of the beam = I/z	in3	(mm3)
z =	distance from neutral axis to extreme fiber (edge)	inches	(mm)

• Please note letter "l" (lower case "L") is different than "I" (Moment of Inertia).
• Deflections apply only to constant cross sections along entire length.

References:

• Any Machinery's Handbook published since 1931 or,
• Machinery's Handbook, 21st Edition, Page 405 or,
• Machinery's Handbook, 23st Edition, Page 261 or,
• Machinery's Handbook, 27st Edition, Page 262

Related

• Beam Deflection Equations / Calculator with End Overhanging Supports and a Single Load
• Beam Deflection Equations / Calculator Cantilevered Beam with One Load Applied at End
• Beam Deflection Equations / Calculator Cantilevered Beam with Uniform Load
• Beam Deflection Equations / Calculator Supported on One End, Rigid one End With Uniform Load
• Beam Deflection Equations / Calculator Cantilevered Beam with Load at Location Between Support and Load
• Beam Deflection Equations / Calculator Free and Guided on One End, Rigid one End With Single Load
• Beam Stress & Deflection Equations / Calculation - Both Ends Overhanging and Supported Unsymmetrical with Uniform Load
• Beam Stress Equations / Calculator - Both Ends Overhanging Supports, Load at any Point Between
• Structural Beam Stress Deflection Equations / Calculation - Fixed at One End, Supported at the Other, Load at Center
• Beam Deflection Equations / Calculator Cantilevered Beam with One Load Applied at End