Related Resources: calculators
Drop Load Beam Stress Equations and Calculator
Stress and Deflection of Beams
Analysis and Engineering
Strength of Materials
Stress from Drop Load of Beam Supported on Both Ends and Struck in the Center. Stresses produced by shock loads.
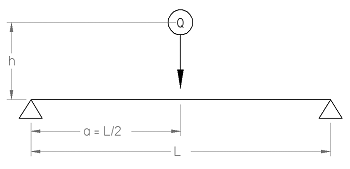
Preview Stresses Produced in Beam by Shock Loads
![]()
or, approximately
![]()
Where:
Q = Weight of dropped mass (N)
E = Modulus of Elasticity (N/mm2)
I = Area Moment of Inertia (mm4)
L = Length of beam (mm)
a = Distance from support (mm)
h = Height distance (mm)
p = Stress (N/mm2)
Stresses in Beams Produced by Shocks.
Any elastic structure subjected to a shock will deflect until the product of the average resistance, developed by the deflection, and the distance through which it has been overcome, has reached a value equal to the energy of the shock. It follows that for a given shock, the average resisting stresses are inversely proportional to the deflection. If the structure were perfectly rigid, the deflection would be zero, and the stress infinite. The effect of a shock is, therefore, to a great extent dependent upon the elastic property (the springiness) of the structure subjected to the impact.
The energy of a body in motion, such as a falling body, may be spent in each of four ways:
1) In deforming the body struck as a whole.
2) In deforming the falling body as a whole. 3) In partial deformation of both bodies on the surface of contact (most of this energy will be transformed into heat). 4) Part of the energy will be taken up by the supports, if these are not perfectly rigid and inelastic.
How much energy is spent in the last three ways it is usually difficult to determine, and for this reason it is safest to figure as if the whole amount were spent as in Case 1. If a reliable judgment is possible as to what percentage of the energy is spent in other ways than the first, a corresponding fraction
One investigation into the stresses produced by shocks led to the following conclusions:
1) A suddenly applied load will produce the same deflection, and, therefore, the same stress as a static load twice as great; and
2) The unit stress p (see formulas in Table 1, "Stresses Produced in Beams by Shocks") for a given load producing a shock, varies directly as the square root of the modulus of elasticity E, and inversely as the square root of the length L of the beam and the area of the section.
Thus, for instance, if the sectional area of a beam is increased by four times, the unit stress will diminish only by half. This result is entirely different from those produced by static loads where the stress would vary inversely with the area, and within certain limits be practically independent of the modulus of elasticity.
Reference:
Machinery's Handbook, 27th Edition Stresses Produced in Beam by Shocks