Shock Loading Helical Springs Formulas and Calculator

Related Resources: calculators

Shock Loading Helical Springs Formulas and Calculator

Manufacturing Design
Spring Design and Engineering Resources

Stresses in Helical Springs Produced by Shocks Formulas and Calculator

Preview: Stresses in Helical Springs Produced by Shocks Calculator

Stresses in Helical Springs Produced by Shocks. A load suddenly applied on a spring will produce the same deflection, and, therefore, also the same unit stress, as a static load twice as great. When the load drops from a height h, the stresses are as given in the accompanying Table 1. The approximate values are applicable when the deflection is small as compared with the height h. The formulas show that the fiber stress for a given shock will be greater in a spring made from a square bar than in one made from a round bar, if the diameter of coil is the same and the side of the square bar equals the diameter of the round bar. It is, therefore, more economical to use round stock for springs which must withstand shocks, due to the fact that the deflection for the same fiber stress for a square bar spring is smaller than that for a round bar spring, the ratio being as 4 to 5. The round bar spring is therefore capable of storing more energy than a square bar spring for the same stress.

Round Bar Spring

Fiber (Unit) Stress f Produced by Weight Q Dropped a Height h on a Helical Spring

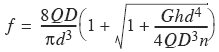
Approximate Value of f Round Bar Spring

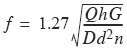
Square Bar Spring

Fiber (Unit) Stress f Produced by Weight Q Dropped a Height h on a Helical Spring

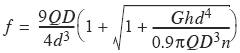
Approximate Value of f Square Bar Spring

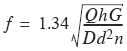
Where:

Q = Weight
G = modulus of elasticity for torsion;
d = diameter or side of bar;
D = mean diameter of spring;
n = number of coils in spring.
f = fiber unit stress

Reference: Machinerys Handbook 29th Edition