Related Resources: beam bending
Structural Beam Stress and Deflection for Non-Engineers
Beam Stress Deflection Equations and Calculators
Structural Beam Stress and Deflection Calculations for Non-Engineers
The following is a procedure to determine the critical design elements of a simple structural configuration being loaded. Please be aware that completing the procedure will not qualify you as a structural engineer or any other kind of engineer. We at Engineers Edge do not take any responsibility for any design failures that may occur. If you're designing anything that if it fails can injure, kill or cause extreme financial loss - hire a licensed structural engineer to do the design for you. Be careful, go slow, remember safety before money, and think. Additionally... if you have a question, post that question within the Engineering Forums, please do not email, feedback, call us.
First, Visit our Structural Beam Defection and Stress web page menu and see if we have the loading configuration euqation and calculator that best fits your application. If we do, awesome bookmark, remember or whatever.
If you're good with math do the calculations by hand if not and/or you need a double check use the automated calculators. You may need to become a Premium Member to use the calculator (this helps us pay for the web site and will make your job WAY easier).
Second, determine what your maximum applied load will be in pounds (lbs) or Newton's (N).
Third, what is the maximum length of your loaded structural member? inches, ft or millimeter (mm)
Forth, decide what material you would like to use in your design - wood, aluminum, steel, etc. This is just a starting materiel guess. You may actually need to use stronger, ore expensive, different geometry in your final design so this is just a guess to ge you started. Engineering design typically is a iterative process - which means that you are going to try several configurations until the numbers look good.
Once you know what material you want to use get and record the following for that material:
Modulus of Elasticity or Young's Modulus is a constant (number) that characterizes the materials tendency to deflect or deform under loading. Sometimes called the elastic modulus. given in psi or N/mm2
Yield Strength is simply the stress at which the structural member begins to permanently stretch or deform when loading is applied. You are going to want to design your structural member so that the maximum stress in service is well below the Yield Strength as this number and for that matter the Proportional limit is a bad place to be. We don't want failures, bending or anything breaking!
Here's the challenge with the the modulus of elasticity and Yield Strength. You are going to look up some material and get a generic typical value not a certified or guaranteed value. Unless you purchase trace-ability on your material you don't really know what you have. This is why it is always best to over design the structure and then test load (Proof Load) your as-built apparatus.
Fifth, decide what geometry or structural shape you want to use. Again, this is a starting geometry guess. You may may hit the bulls eye first attempt or need to design for a larger or different shape. Once you know what geometry you think will work get the Area Moment of Inertia for that geometry. Here's some links:
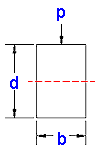
The Area Moment of Inertia that you want is that where the load is perpendicular to the section line as follows:
Ok, so now you should have all the basic design information you need to get started, let's review:
- Maximum applied load (estimated or real) this is equal to the maximum load being lifted.
- Loading Configuration - know the equations and/or use calculator.
- Length,
- Material,
- Modulus of Elasticity (Young's Modulus)
- Yield Strength
- Area Moment of Inertia for geometry being loaded.
- Distance to the Nuetral axis
Design example:
Let's do a simple structural design tha will lift an engine out and into our expensive project car in our garage.
Engine weight according to manufacturers specifications = 300 lbs.
Block and tackle mounted on the beam properly that we are going to use to lift the engine (rated far above 300 lbs) weights 40 lbs.
Chain attached to engine front and back to keep lifting action even (10 lbs).
Misc. hardware (5 lbs).
Therefore, we are going to lift a maximum of: 300 + 40 + 10 + 5 = 355 lbs
I suggest a block and tackle rated at not less than 1.5 x tha maximum load you are lifting.
The plan is a simple beam placed on top of very sturdy concrete block wall across the garage. We plan to roll the car body underneath the engine to install. Therefore the loading configuration is like this:
Let's use this calculator:
Stress and Deflection Beam Supported both Ends Load in Center Equation and/or Calculator
The beam we want to use will be made out of wood, probably pressure treated pine from the local hardware store. Therefore:
Modulus of Elasticity for Wood = .99 x 106 ( 990,000) psi (pounds per square inch)
Yield Strength - This is tricky for wood as there generally is not a yield specification available. What we will use is the data for the "Modulus of Rupture " specification which for pine, eastern is = approximately 4,900 psi.. Modulus of Rupture is the theoretical value where the wood breaks or fails - not good for our car or engine if this happens.
So, let's try a 4 x 4 standard wood beam which is actually a 3.5" x 3.5"
Therefore, using this calculator: Area Moment Square Section the Area Moment of Inertia is = 12.50 in4
The beam need to be wider than the car so, let's make it 7 ft or 84 inches from support to support.
The distance to the neutral axis (Extreme Point) is one half the thickness perpendicular to the load of my cross section or 3.5" / 2 = 1.75 in
So, here's my calculations:
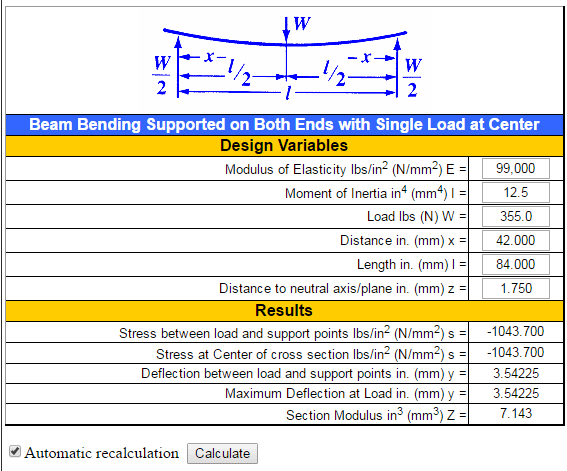
My calculated stress applied is -1,043.7 psi and my deflection is 3.54225 inches
So, the applied stress is 1,043.7 psi and this is less than my Modulus of Rupture which is 4,900 psi. Therefore I have a Factor of Safety = Failure Load / Applied Load = 4.395.
In theory, this should work though I would suggest that due to the deflection of 3.54 inches a higher Factor of Safety would be better as the less a beam deflects the better as large deflections can lead to all kinds of special problems that I'm not going to include here.
If you stack two standard wood 4" x 4" on top of each other you get an Area moment of inertia calculated = 100

Recalculating the stress and deflection I get:
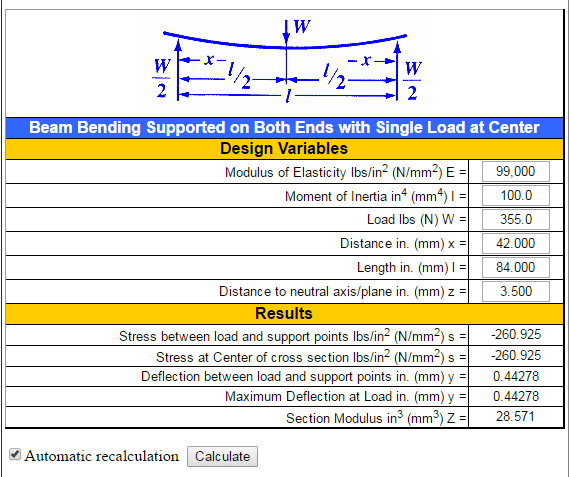
Stress applied = 260.925 psi and a deflection of .44278 inches. Low deflection and stress and all I needed was another 4 x 4.
This should work good and the risk of failure is minimized - GO FOR IT!
In closing :
Since you went through all this effort I recommend that you build your apparatus and proof load it. Carefully apply 355 lbs at the center and measure the actual deflection. Verify the actual sizes of your 4 x 4's. Then compare the actual deflection and sizes to the calculated deflection and beam sizes you used - there will likely be a difference hopefully not too much. If you are curious, come back to the beam deflection and stress calculator and modify the Modulus of Elasticity until you get the same deflection by calculation. This will give you a hint of what the wood engineering properties really are. Wood varies from lot to lot.
This is a very basic approach to determine the theoretical stress and deflection of a particular loading configuration. Know that engineering materials are never what they claim to be and that it is way easier and smarter to over engineer than to engineer it "Just Right".
Related
- Beam Supported on Both Ends Uniform Loading Deflection and Stress Stress, Deflection Equation and Calculator using total applied load and line load.
- Beam Calculator Cantilevered Beam with One Load Applied at End Deflection and Stress Structural Beam Deflection, Stress, Bending Equations and calculator for a Cantilevered Beam with One Load Applied at End.
- Beam Distributed Load Deflection, Shear, Deflection and Stress Equations and Calculator Beam Deflection, Shear and Stress Equations and Calculator for a Beam supported One End, Pin Opposite End and Partial Distributed Load
- Calculator for a Beam supported One End, Pin Opposite End and Single Moment at End Applied Deflection and Stress Calc Beam Deflection, Shear and Stress Equations and Calculator for a Beam supported One End, Pin Opposite End and Single Moment at End Applied
- Stress & Deflection Deflection Equations and Calculator Beam Supported Uniform loading Applied on Cantilevered End Stress Deflection Equations and Calculator Beam Supported Uniform loading Applied on Cantilevered End