Related Resources: calculators
Balancing Rotating Fixtures Turning Operations on a Lathe Formulas and Calculator
Machine Design and Applications
Balancing Rotating Lathe Fixtures. Lathe fixtures rotating at a high speed require balancing. Often it is assumed that the center of gravity of the workpiece and fixture, and of the counterbalancing masses are in the same plane; however, this is not usually the case. Counterbalancing masses are required in two separate planes to prevent excessive vibration or bearing loads at high speeds.
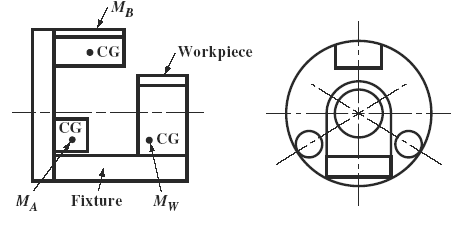
Figure 1
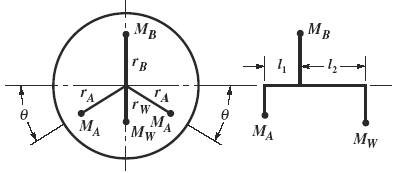
Figure 2
Usually a single counterbalancing mass is placed in one plane selected to be 180 degrees directly opposite the combined center of gravity of the workpiece and the fixture. Two equal counterbalancing masses are then placed in the second counterbalancing plane, equally spaced on each side of the fixture. Referring to Fig. 2, the two counterbalancing masses MA and the two angles θ are equal. For the design in this illustration, the following formulas can be used to calculate the magnitude of the counterbalancing masses. Since their angular positions are fixed by the design, they are not calculated.
MB = ( Mwrw(l1 + l2 ) / ( rB l1 )
MA = ( MBrB - Mwrw ) / (2 rA sinθ )
In these formulas Mw and rw denote the mass or weight and the radius of the combined center of gravity of the workpiece and the fixture.
Related:
- Counterbalancing Several Masses Located in a Single Plane Formulas and Calculator
- Critical Speeds of Rotating Shafts and Mass Review
- Trailer Weight and Balance Equations and Calculator
Reference:
Machinerys Handbook, 29th Edition