Related Resources: calculators
Concrete Modulus of Elasticity Equations and Calculator
Civil Engineering and Design
Strength of Materials Basics and Equations | Mechanics of Materials
Concrete Secant Modulus of Elasticity Equations and Calculator
The modulus of elasticity (also known as Young’s modulus) is defined as the ratio of stress to strain in the elastic region. Unlike steel, the modulus of elasticity of concrete varies with compressive strength. Since the slope of the stress-strain curve varies with the applied stress, there are several ways of calculating the modulus of elasticity. Figure 1 shows a typical stress-strain curve for concrete with the initial modulus, the tangent modulus, and the secant modulus indicated.
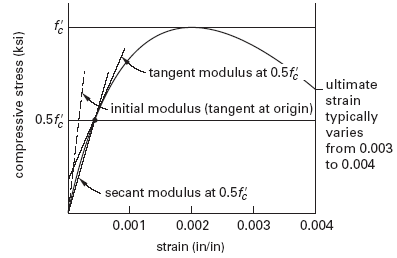
Figure 1, Concrete Stress Strain Curve
The secant modulus of elasticity is specified by ACI 318 for use with specific weights that are between 90 lbf/ft3 and 160 lbf/ft3 (1440 kg/m3 and 2560 kg/m3). Equation 1 & 2 are used for both instantaneous and long term deflection calculations. ωc is in lbf/ft3(kg/m3), and Ec and f'c are in lbf/in2 (MPa) [ACI 318 Sec. 8.5.1].
Secant modulus of elasticity
Eq. 1, SI Units
Ec = 0.043 ωc1.55 (f'c)0.5
Eq. 2, U.S.
Ec = 33 ωc1.55 (f'c)0.5
For normal weight concrete, ACI 318 uses Eq. 3 & 4, which corresponds to a specific weight of approximately 145 lbf/ft3 (2320 kg/m3) [ACI 318 Sec. 8.5.1].
Eq. 3, SI
Ec = 5,000 (f'c)0.5
Eq. 4, U.S.
Ec = 57,000 (f'c)0.5
Where:
ωc = specific weight, lbf/ft3(kg/m3)
f'c = compressive strength of concrete, lbf/in2 (MPa)
Ec = modulus of elasticity (young's modulus), lbf/in2 (MPa)
Reference
Civil Engineering Reference Manual, Fifteenth Edition, Michael R. Lindeburg, PE
Related
- Modulus of Elasticity , Youngs Modulus Table and Calculator
- Bulk Modulus for Materials Metals and Liquids
- Young's Modulus (Elastic Modulus ) Equation
- Ultimate Strength, Modulus of Elasticity , Yield Point of Metals Table Chart
- Concrete Foundation Anchor Bolts Design
- Manual of Concrete Design ACI
- Reinforced Concrete Beam Design to BS8110 Calculator
- Reinforced Concrete Beam Design per. ACI 318-08 Calculator Spreadsheet
- Concrete Pad Foundation Design Spreadsheet Calculator
- Concrete Structural Designers Guide
- Reinforced Concrete Handbook
- Concrete Creep Shrinkage Factors and Tensile Strength Calculation
- Concrete Rectangular Beam Section Analysis Calculator
- Rectangular Concrete Beam and Slab Section Analysis
- Concrete Anchor Tension Pull Away Calculator ACI 318-02