Related Resources: calculators
Two Bars Different Temperatures Stress Calculator and Equations
Two Bars At Different Temperatures Stress Calculator and Equations
The bars are attached such that the cold bar restrains the expansion of the hot bar. The bars remain straight with no bending.
Eq. 1
Eq. 2
Eq. 3
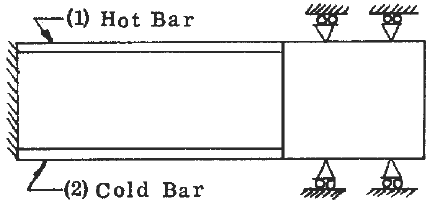
Figure 1 Two bars at different Temperatures
Where
A1 = Cross section area bar 1
A2 = Cross section area bar 2
E1 = modulus of elasticity bar 1
E2 = modulus of elasticity bar 2
α1 = coefficient of thermal expansion bar 1
α2 = coefficient of thermal expansion bar 1
T0 = initial (reference) temperature
T1 = temperature bar 1
T2 = temperature bar 2
σ1 = stress bar 1
σ2 = stress bar 2
- Bell Helicopter Structural Design Manual, 1977
Related
- Bar Restrained With Spring Uniform Heat Applied Calculator
- Bar Restrained One End and Gap on Other Formula and Calculator
- Restrained Beam Thermal Expansion Force Axial Stress Calculator
- Linear Thermal Expansion Equation and Calculator
- Pipe Expansion Thermal Loop Equations and Calculator
- Fastener Thermal Expansion Equation and Calculator
- Compression Tension Stress Linear Thermal Expansion Equation and Calculator
- Thermal Linear Expansion of AISI 303 Stainless Steel
- Stress Concentration Cylinder feature with Axial Loading Stress concentration on a selected radius of a shaft with axial loading.
- Solid Shaft Equivalent of Hollow Shaft of Same Length Equal Strength Formula and Calculator
- Cylinder Interference Press Fit Design Equations and Calculator
- Torsion Stress Calculator and Equations Torsion is the twisting of an object due to an applied torque . It is expressed in newton meters (N-m) or foot-pound force (ft-lbf).